
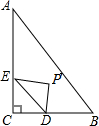
 如图,∠C=90°,BC=3,AB=5,点D是BC上一动点,CD=x,DE∥AB交AC于点E,以直线DE为轴作△CDE的轴对称△PDE,△PDE落在△ABC内的面积为y,则下列能刻画y与x之间函数关系的图象是( )
如图,∠C=90°,BC=3,AB=5,点D是BC上一动点,CD=x,DE∥AB交AC于点E,以直线DE为轴作△CDE的轴对称△PDE,△PDE落在△ABC内的面积为y,则下列能刻画y与x之间函数关系的图象是( )| A. |  | B. | 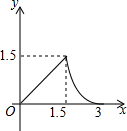 | C. | 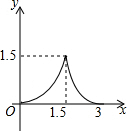 | D. | 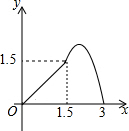 |
分析 根据DE∥AB可将EC用x表示出来,从而可以得到y与x的关系式,要将面积分成点P在△ABC内及△ABC外两种情况进行分析,就可以得到正确的函数图象.
解答 解:∵∠C=90°BC=3,AB=5∴AC=4
∵DE∥AB,∴$\frac{CD}{CB}=\frac{CE}{AC}$,
∵CD=x∴$\frac{x}{3}=\frac{EC}{4}$ 化简得 EC=$\frac{4}{3}$x
当点P落在△ABC内部时,y=S△PDE=$\frac{1}{2}•x•\frac{4}{3}x$=$\frac{2}{3}$x2(0≤x≤$\frac{3}{2}$),此时图象应为抛物线,且y随x的增大而增大;
当点P落在AB上时,如图1,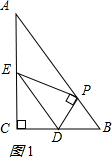
∵DE∥AB,
∴∠DEF=∠EPA,∠CED=∠A
∵∠CED=∠DEP EC=EP,
∴∠A=∠EPA,
∴AE=EP=EC=2,
同理可得DP=DB=DC=$\frac{3}{2}$,
∴y=$\frac{1}{2}$×2×$\frac{3}{2}$=$\frac{3}{2}$,即当x=$\frac{3}{2}$时,y=$\frac{3}{2}$;
当点P落在AB外时,设PE与AB交于点M,PD与AB交于点N,如图2,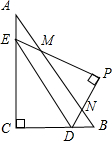
同理可得EM=AE DN=DB,
∵AE=4-EC BD=3-CD
∴PM=PE-ME=$\frac{4}{3}$x-(4-$\frac{4}{3}$x)=$\frac{8}{3}$x-4,PN=PD-ND=x-(3-x)=2x-3,
∴y=S△PDE-S△PMN=$\frac{2}{3}$x2-$\frac{1}{2}×(\frac{8}{3}x-4)(2x-3)$=-2x2+8x-6=-2(x-2)2+2($\frac{3}{2}$<x≤3)
当x=2时,y有最大值为2.则图象为抛物线,应先上升再下降.
故选:A.
点评 本题考查了折叠的性质、等腰三角形性质及平行线分线段成比例定理,解题的关键是要通过平行得到三角形边之间的关系,根据点动后形成的不同图形来进行分类讨论.


 名师点拨卷系列答案
名师点拨卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
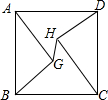
| A. | $\frac{8\sqrt{3}}{5}$ | B. | 2$\sqrt{2}$ | C. | $\frac{14}{5}$ | D. | 10-5$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com