练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    化简并求值

    化简：4－(2x＋6－10x3－12x2)＋(3－6x2＋12x＋18x4)，并求当x＝0.1时，这个代数式的值．

    答案：
    解析：

    原式＝2＋3x＋4x2＋5x3＋6x4，2.3456


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    21、2008年5月31日北京奥运圣火在武汉传递，圣火传递路线分为两段，其中在市区的一段传递路程为700 （a-l）米，在郊区的一段传递路程为．（801a+2399）米．设圣火在武汉的传递总路程为s米．
    （1）用含a的整式表示s，并将结果化简；  （2）已知a=ll，求s的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：阅读理解

    先阅读，再化简求值：
    （1）在化简
    		5-2
    		6
    的过程中．小张和小李的化简结果不一样：
    小张的化简过程如下：
    原式=
    		2-2
    		2×3
    +3
    =
    		(
    		2
    )2-2
    		2
    ×
    		3
    +(
    		3
    )2
    =
    		(
    		2
    -
    		3
    )2
    =
    		2
    -
    		3

    小李的化简过程如下：
    原式=
    		3-2
    		2×3
    +2
    =
    		(
    		3
    )2-2
    		3
    ×
    		2
    +(
    		2
    )2
    =
    		(
    		3
    -
    		2
    )2
    =
    		3
    -
    		2

    请判断谁的化简结果是正确的，谁的化简结果是错误的，并说明理由？
    （2）请你利用上面所学的方法，化简求值：已知x=
    		6-2
    		5
    ，求(
    1
    x-2
    +
    1
    x+2
    )×
    x2-4
    2(x-1)
    的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：阅读理解

    先阅读再化简求值：
    （1）在化简
    		5-2
    		6
    的过程中．小张和小李的化简结果不一样：小张的化简过程如下：
    原式=
    		2-2
    		2×3
    +3
    =
    		(
    		2
    )2+2
    		2
    ×
    		3
    +(
    		3
    )2
    =
    		(
    		2
    -
    		3
    )2
    =
    		2
    -
    		3

    小李的化简过程如下：
    原式=
    		3-2
    		2×3
    +2
    =
    		(
    		3
    )2+2
    		3
    ×
    		2
    +(
    		2
    )2
    =
    		(
    		3
    -
    		2
    )2
    =
    		3
    -
    		2

    请判断谁的化简结果是正确的，谁的化简结果是错误的，并说明理由？
    （2）请你利用上面所学的方法，化简求值：已知x=
    		6-2
    		5
    ，求x2+2x-3的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

     根据对北京市相关的市场物价调研，预计进入夏季后的某一段时间，某批发市场内的

    甲种蔬菜的销售利润y1（千元）与进货量x（吨）之间的函数的图象如图①所示，乙种蔬菜的销售利润y2（千元）与进货量x（吨）之间的函数的图象如图②所示.

    （1）分别求出y1、y2与x之间的函数关系式；

    （2）如果该市场准备进甲、乙两种蔬菜共10吨，设乙种蔬菜的进货量为t吨，写出这两种蔬菜所获得的销售利润之和W（千元）与t（吨）之间的函数关系式，并求出这两种蔬菜各进多少吨时获得的销售利润之和最大，最大利润是多少？

     

     

     

     

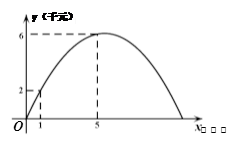
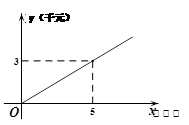
    【解析】（1）y1=kx的图象过点（3，5.），求出k,y2=ax2+bx的图象过点(1,2),(5,6) 求出a,b

    （2）由等量关系“两种蔬菜所获得的销售利润之和=甲种蔬菜的销售利润+乙种蔬菜的销售利润”即可列出函数关系式；

    用配方法化简函数关系式即可求出w的最大值．

     

    查看答案和解析>>

    科目：初中数学 来源：2011-2012学年北京市朝阳区中考一模数学卷（解析版） 题型：解答题

     根据对北京市相关的市场物价调研，预计进入夏季后的某一段时间，某批发市场内的

    甲种蔬菜的销售利润y1（千元）与进货量x（吨）之间的函数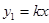的图象如图①所示，乙种蔬菜的销售利润y2（千元）与进货量x（吨）之间的函数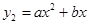的图象如图②所示.

    （1）分别求出y1、y2与x之间的函数关系式；

    （2）如果该市场准备进甲、乙两种蔬菜共10吨，设乙种蔬菜的进货量为t吨，写出这两种蔬菜所获得的销售利润之和W（千元）与t（吨）之间的函数关系式，并求出这两种蔬菜各进多少吨时获得的销售利润之和最大，最大利润是多少？

     

     

     

     

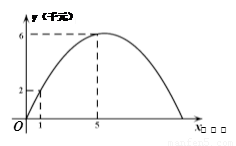
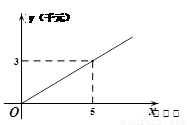
    【解析】（1）y1=kx的图象过点（3，5.），求出k,y2=ax2+bx的图象过点(1,2),(5,6) 求出a,b

    （2）由等量关系“两种蔬菜所获得的销售利润之和=甲种蔬菜的销售利润+乙种蔬菜的销售利润”即可列出函数关系式；

    用配方法化简函数关系式即可求出w的最大值．

     

    查看答案和解析>>

    同步练习册答案