
 完成下面的证明.
完成下面的证明.分析 (1)根据两直线平行,内错角相等以及两直线平行,同旁内角互补,即可得到∠B+∠D=180°.
(2)根据角平分线的定义,即可得到∠1=$\frac{1}{2}$∠ABC,∠2=$\frac{1}{2}$∠A'B'C',再根据∠ABC=∠A′B′C′,即可得出∠1=∠2.
解答 解:(1)证明:∵AB∥CD,
∴∠B=∠C(两直线平行,内错角相等);
∵CB∥DE,
∴∠C+∠D=180°(两直线平行,同旁内角互补).
∴∠B+∠D=180°.
(2)证明:∵BD,B′D′分别是∠ABC,∠A′B′C′的平分线,
∴∠1=$\frac{1}{2}$∠ABC,∠2=$\frac{1}{2}$∠A'B'C'(角平分线的定义).
又∠ABC=∠A′B′C′,
∴$\frac{1}{2}$∠ABC=$\frac{1}{2}$∠A′B′C′.
∴∠1=∠2(等量代换).
故答案为:∠C,两直线平行,内错角相等,两直线平行,同旁内角互补;$\frac{1}{2}$∠A'B'C',角平分线的定义,等量代换.
点评 本题主要考查了平行线的性质以及角平分线的定义的运用,解题时注意:两直线平行,内错角相等;两直线平行,同旁内角互补.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
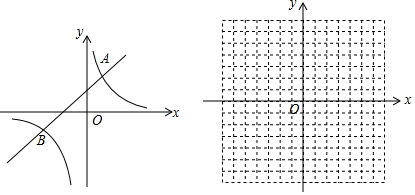
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
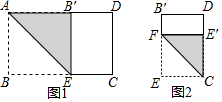 矩形纸片ABCD中,AD=10,AB=a(5<a<10)
矩形纸片ABCD中,AD=10,AB=a(5<a<10)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
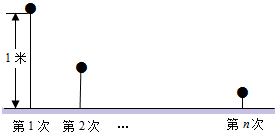 一小球从距地面1m高处自由落下,每次着地后又跳回到原高度的一半再落下.
一小球从距地面1m高处自由落下,每次着地后又跳回到原高度的一半再落下.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
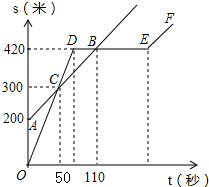 某中学的小明和朱老师一起到一条笔直的跑道上锻炼身体,到达起点后小明做了一会准备活动朱老师先跑,当小明出发时,朱老师已经距起点200米了,他们距起点的距离s(米)与小明出发的时间t(秒)之间的关系如图所示(不完整).根据图中给出的信息,解答下列问题:
某中学的小明和朱老师一起到一条笔直的跑道上锻炼身体,到达起点后小明做了一会准备活动朱老师先跑,当小明出发时,朱老师已经距起点200米了,他们距起点的距离s(米)与小明出发的时间t(秒)之间的关系如图所示(不完整).根据图中给出的信息,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 班级 | 最高分 | 平均分 | 中位数 | 众数 | 方差 |
| 九(1)班 | 100 | 94 | b | 93 | 12 |
| 九(2)班 | 99 | a | 95.5 | 93 | 8.4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com