Question

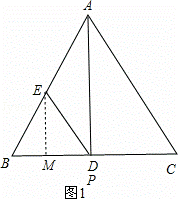
如图，在△ABC中，AB=AC=10，BC=12，D，E分别是边BC，AB的中点，P是BC边上的动点（不与B，C重合）．设BP=x．

（1）当x=6时，求PE的长；

（2）当△BPE是等腰三角形时，求x的值；

（3）当AD平分EP时，试判断以EP为直径的圆与直线AC的位置关系，并说明理由．

Answer 1

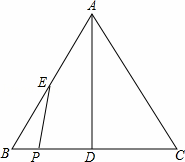
解：（1）∵AB=AC=10，BC=12，D为边BC的中点，

∴BD=CD=6，AD⊥BC，

∴当x=6时，点P在D点处，

∴PE为Rt△ABD斜边上的中线，

∴PE=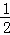AB=5；

（2）∵点E为AB的中点，

∴BE=5，

当BP=BE=5，则x=5；

当EP=EB，作EM⊥BD于M，如图1，则BM=PM，

∵点E为AB的中点，

而EM∥AD，

∴M点为BD的中点，

∴PB=BD=6，

∴x=6；

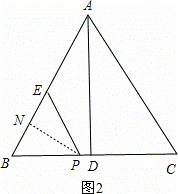
当PB=PE，如图2，作PN⊥BE于N，则BN=EN=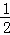BE=，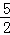

∵∠PBN=∠DBA，

∴Rt△BPN∽Rt△BAP，

∴PB：AB=BN：BD，即x：10=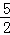：6，

∴x=，

综上所述，当△BPE是等腰三角形时，x的值为5或6或；

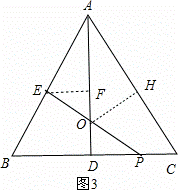
（3）以EP为直径的圆与直线AC相交．理由如下：

EP交AD于O，作OH⊥AC于H，EF⊥AD于F，如图3，

在Rt△ABC中，AB=10，BD=6，

∴AD==8，

∵点E为AB的中点，

而EF∥BD，

∴EF为△ABD的中位线，

∴EF=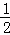BD=3，AF=DF=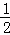AD=4，

∵AD平分EP，

∴OE=OF，

在△OEF和△OPD中

，

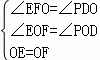∴△OEF≌△OPD，

∴OF=OD，

∴OF=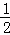DF=2，

∴AO=AF+OF=6，

在Rt△OEF中，EF=3，OF=2，

∴OE==，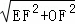

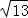∵∠OAH=∠CAD，

∴Rt△AOH∽Rt△ACD，

∴OH：CD=AO：AC，即OH：6=6：10，解得OH=，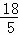

∵OE=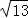==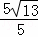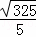，OH===，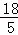

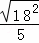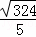∴OE＞OH，

∴以EP为直径的圆与直线AC相交．