
 如图,在△ABC中,AB=9,AC=6,BC=12,点M在AB边上,且AM=3,过点M作直线MN与AC边交于点N,使截得的三角形与原三角形相似,则MN=4或6.
如图,在△ABC中,AB=9,AC=6,BC=12,点M在AB边上,且AM=3,过点M作直线MN与AC边交于点N,使截得的三角形与原三角形相似,则MN=4或6. 分析 分别利用,当MN∥BC时,以及当∠ANM=∠B时,分别得出相似三角形,再利用相似三角形的性质得出答案.
解答 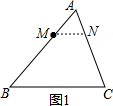 解:如图1,当MN∥BC时,
解:如图1,当MN∥BC时,
则△AMN∽△ABC,
故$\frac{AM}{AB}$=$\frac{AN}{AC}$=$\frac{MN}{BC}$,
则$\frac{3}{9}$=$\frac{MN}{12}$,
解得:MN=4,
如图2所示: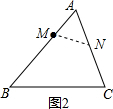 当∠ANM=∠B时,
当∠ANM=∠B时,
又∵∠A=∠A,
∴△ANM∽△ABC,
∴$\frac{AM}{AC}$=$\frac{MN}{BC}$,
即$\frac{3}{6}$=$\frac{MN}{12}$,
解得:MN=6,
故答案为:4或6.
点评 此题主要考查了相似三角形判定,正确利用分类讨论得出是解题关键.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,将△ABC沿着过AB中点D的直线折叠,使点A落在BC边上的A1处,称为第1次操作,折痕DE到BC的距离记为h1;还原纸片后,再将△ADE沿着过AD中点D1的直线折叠,使点A落在DE边上的A2处,称为第2次操作,折痕D1E1到BC的距离记为h2;按上述方法不断操作下去…,经过第5次操作后得到的折痕D4E4,到BC的距离记为h5;若h1=1,则h5的值为( )
如图,将△ABC沿着过AB中点D的直线折叠,使点A落在BC边上的A1处,称为第1次操作,折痕DE到BC的距离记为h1;还原纸片后,再将△ADE沿着过AD中点D1的直线折叠,使点A落在DE边上的A2处,称为第2次操作,折痕D1E1到BC的距离记为h2;按上述方法不断操作下去…,经过第5次操作后得到的折痕D4E4,到BC的距离记为h5;若h1=1,则h5的值为( )| A. | $2-\frac{1}{2^4}$ | B. | $\frac{1}{2^4}$ | C. | $1-\frac{1}{2^5}$ | D. | $\frac{1}{2^5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,BC=4,D、E分别是边AB和AC的中点,下面结论中不正确的是( )
如图,在△ABC中,BC=4,D、E分别是边AB和AC的中点,下面结论中不正确的是( )| A. | DE=2 | |
| B. | △ADE的面积与△ABC的面积之比为1:4 | |
| C. | △ADE∽△ABC | |
| D. | △DEC的周长与△ABC的周长之比为1:2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com