
【题目】当m,n是正实数,且满足m+n=mn时,就称点P(m,![]() )为“完美点”,已知点A(0,5)与点M都在直线y=﹣x+b上,点B,C是“完美点”,且点B在线段AM上,若MC=
)为“完美点”,已知点A(0,5)与点M都在直线y=﹣x+b上,点B,C是“完美点”,且点B在线段AM上,若MC=![]() ,AM=4
,AM=4![]() ,求△MBC的面积
,求△MBC的面积
【答案】![]()
【解析】分析:由m+n=mn变式为![]() 可知P(m,m1),所以在直线y=x1上,点点A(0,5)在直线y=x+b上,求得直线AM:y=x+5,进而求得B(3,2),根据直线平行的性质从而证得直线AM与直线y=x1垂直,然后根据勾股定理求得BC的长,从而求得三角形的面积.
可知P(m,m1),所以在直线y=x1上,点点A(0,5)在直线y=x+b上,求得直线AM:y=x+5,进而求得B(3,2),根据直线平行的性质从而证得直线AM与直线y=x1垂直,然后根据勾股定理求得BC的长,从而求得三角形的面积.
详解:
∵m+n=mn且m,n是正实数,
∴![]() ,即
,即![]()
∴P(m,m1),
即“完美点”B在直线y=x1上,
∵点A(0,5)在直线y=x+b上,
∴b=5,
∴直线AM:y=x+5,
∵“完美点”B在直线AM上,
∴由![]() 解得
解得![]()
∴B(3,2),
∵一、三象限的角平分线y=x垂直于二、四象限的角平分线y=x,而直线y=x1与直线y=x平行,直线y=x+5与直线y=x平行,
∴直线AM与直线y=x1垂直,
∵点B是直线y=x1与直线AM的交点,
∴垂足是点B,
∵点C是“完美点”,
∴点C在直线y=x1上,
∴△MBC是直角三角形,
∵B(3,2),A(0,5),
∴![]()
∵![]()
∴![]()
又∵![]() ,
,
∴BC=1,
∴![]()
点睛:本题考查了一次函数的性质,直角三角形的判定,勾股定理的应用以及三角形面积的计算等,判断直线垂直,借助正比例函数是本题的关键.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,D、E为⊙O上位于AB异侧的两点,连接BD并延长至点C,使得CD=BD,连接AC交⊙O于点F,连接AE、DE、DF.
(1)证明:∠E=∠C;
(2)若∠E=55°,求∠BDF的度数;
(3)设DE交AB于点G,若DF=4,cosB=![]() ,E是弧AB的中点,求EGED的值.
,E是弧AB的中点,求EGED的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上,四个不同的点![]() 分别表示有理数
分别表示有理数![]() ,且
,且![]() .
.
(1)如图1,![]() 为线段
为线段![]() 的中点,
的中点,

①当点![]() 与原点
与原点![]() 重合时,用等式表示
重合时,用等式表示![]() 与
与![]() 的关系为 ;
的关系为 ;
②求点![]() 表示的有理数
表示的有理数![]() 的值(用含
的值(用含![]() 的代数式表示);
的代数式表示);
(2)已知![]() ,
,
①若三点![]() 的位置如图所示,请在图中标出点
的位置如图所示,请在图中标出点![]() 的位置;
的位置;

②![]() 的大小关系为 (用“
的大小关系为 (用“![]() ”连接)
”连接)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中学生骑电动车上学给交通安全带来隐患,为了解某中学2 500个学生家长对“中学生骑电动车上学”的态度,从中随机调查400个家长,结果有360个家长持反对态度,则下列说法正确的是( )
A. 调查方式是普查 B. 该校只有360个家长持反对态度
C. 样本是360个家长 D. 该校约有90%的家长持反对态度
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A从原点出发沿数轴向左运动,同时,点B也从原点出发沿数轴向右运动,3秒后,两点相距15个单位长度.已知点B的速度是点A的速度的4倍(速度单位:单位长度/秒).
![]()
(1)求出点A、点B运动的速度,并在数轴上标出A、B两点从原点出发运动3秒时的位置;
(2)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动,几秒时,原点恰好处在点A、点B的正中间?
(3)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动时,另一点C同时从B点位置出发向A点运动,当遇到A点后,立即返回向B点运动,遇到B点后又立即返回向A点运动,如此往返,直到B点追上A点时,C点立即停止运动.若点C一直以20单位长度/秒的速度匀速运动,那么点C从开始运动到停止运动,行驶的路程是多少个单位长度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,函数y=kx+b(k≠0)的图象经过点B(2,0),与函数y=2x的图象交于点A,则不等式0<kx+b<2x的解集为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将正整数1至2019按照一定规律排成下表:

记aij表示第i行第j个数,如a14=4表示第1行第4个数是4.
(1)直接写出a42=_________, a53=_________;
(2)①如果aij=2019,那么i=_________, j =_________;②用i,j表示aij=_____________;
(3) 将表格中的5个阴影格子看成一个整体并平移,所覆盖的5个数之和能否等于2027.若能,求出这5个数中的最小数,若不能说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
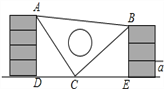
【题目】课间,小明拿着老师的等腰三角板玩,不小心掉到两墙之间,如图.
(1)求证:△ADC≌△CEB;
(2)从三角板的刻度可知AC=25cm,请你帮小明求出砌墙砖块的厚度a的大小(每块砖的厚度相等).
查看答案和解析>>
科目:初中数学 来源: 题型:
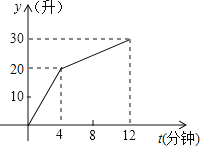
【题目】一个有进水管和一个出水管的容器,每分钟的进水量和出水量都是常数.从某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水.如图表示的是容器中的水量y(升)与时间t(分钟)的图象.
(1)当4≤t≤12时,求y关于t的函数解析式;
(2)当t为何值时,y=27?
(3)求每分钟进水、出水各是多少升?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com