在对25个数据进行整理的频数分布表中.各组的频数之和等于 .各组的频率之和等于．题目和参考答案——青夏教育精英家教网—

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

科目：初中数学 来源： 题型：

十二五期间，重庆将继续建设“五个重庆”，并以“民生”作为政府工作的首要目标，为尽快缩短城乡差距，在“两翼”地区实施万元增收计划，学农的大学毕业生小王自主创业，在政府的帮助下，引进一种种苗，这种种苗既可以用来观赏，同时还能很好吸收二氧化碳，用来改变空气质量，因此有很好的市场前景．去年销售的这种种苗每棵的售价y（元）与月份x之间满足一次函数关系y=-x+62（1≤x≤12且为整数），而去年的月销量p（棵）与月份x之间成某种函数关系，其中四个月的销售情况如下表：

月份x	1月	2月	3月	6月
月销量p（单位：棵）	500	600	700	1000

（1）判断p与x满足我们学过的哪种函数关系？求出函数关系式并验证你的判断．
（2）求该种苗在去年哪个月的销售额最大？最大为多少元？
（3）由于气候等条件的影响，今年1月该种苗的销量比去年12月下降25%．若将今年1月售出的种苗全部进行移栽，则移栽当年的存活率为（1-n%），且平均每株已成活的种苗可吸碳1.6千克，随着该种苗对环境的适应和生长，预计今年成活的种苗明年的成活率为（1-0.2n%），每株已成活种苗的吸碳能力增加0.5n%，未成活种苗在其成活期间吸碳量忽略不计的情况下，预计明年的吸碳量比今年提高2%，求n的整数值．
（参考数据：（

203

≈14.248，

205

≈14.318，

206

≈14.353）

查看答案和解析>>

科目：初中数学 来源： 题型：

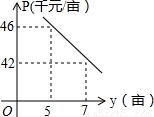
为响应薄熙来书记建设“森林重庆”的号召，某园艺公司从2010年9月开始积极进行植树造林．该公司第x月种植树木的亩数y（亩）与x之间满足y=x+4，（其中x从9月算起，即9月时x=1，10月时x=2，…，且1≤x≤6，x为正整数）．由于植树规模扩大，每亩的收益P（千元）与种植树木亩数y（亩）之间存在如图（25题图）所示的变化趋势．
（1）根据如图所示的变化趋势，直接写出P与y之间所满足的函数关系表达式；
（2）行动实施六个月来，求该每月收益w（千元）与月份x之间的函数关系式，并求x为何值时总收益最大？此时每亩收益为多少？
（3）进入植树造林的第七个月，政府出台了一项激励措施：在“植树造林”过程中，每月植树面积与第六个月植树面积相同的部分，按第六月每亩收益进行结算；超出第六月植树面积的部分，每亩收益将按第六月时每亩的收益再增加0.6m%进行结算．这样，该公司第七月植树面积比第六月增加了m%．另外，第七月时公司需对前六个月种植的所有树木进行保养，除去成本后政府给予每亩4m%千元的保养补贴．最后，该公司第七个月获得种植树木的收益和政府保养补贴共702千元．请通过计算，估算出m的整数值．（参考数据：42²=1764，43²=1849，44²=1936）．

查看答案和解析>>

科目：初中数学 来源：2011-2012学年重庆市南岸区九年级（上）期末数学试卷（解析版） 题型：解答题

为响应薄熙来书记建设“森林重庆”的号召，某园艺公司从2010年9月开始积极进行植树造林．该公司第x月种植树木的亩数y（亩）与x之间满足y=x+4，（其中x从9月算起，即9月时x=1，10月时x=2，…，且1≤x≤6，x为正整数）．由于植树规模扩大，每亩的收益P（千元）与种植树木亩数y（亩）之间存在如图（25题图）所示的变化趋势．
（1）根据如图所示的变化趋势，直接写出P与y之间所满足的函数关系表达式；
（2）行动实施六个月来，求该每月收益w（千元）与月份x之间的函数关系式，并求x为何值时总收益最大？此时每亩收益为多少？
（3）进入植树造林的第七个月，政府出台了一项激励措施：在“植树造林”过程中，每月植树面积与第六个月植树面积相同的部分，按第六月每亩收益进行结算；超出第六月植树面积的部分，每亩收益将按第六月时每亩的收益再增加0.6m%进行结算．这样，该公司第七月植树面积比第六月增加了m%．另外，第七月时公司需对前六个月种植的所有树木进行保养，除去成本后政府给予每亩4m%千元的保养补贴．最后，该公司第七个月获得种植树木的收益和政府保养补贴共702千元．请通过计算，估算出m的整数值．（参考数据：42²=1764，43²=1849，44²=1936）．

查看答案和解析>>

科目：初中数学 来源：2011年重庆市沙坪坝区中考数学模拟试卷（一）（解析版） 题型：解答题

十二五期间，重庆将继续建设“五个重庆”，并以“民生”作为政府工作的首要目标，为尽快缩短城乡差距，在“两翼”地区实施万元增收计划，学农的大学毕业生小王自主创业，在政府的帮助下，引进一种种苗，这种种苗既可以用来观赏，同时还能很好吸收二氧化碳，用来改变空气质量，因此有很好的市场前景．去年销售的这种种苗每棵的售价y（元）与月份x之间满足一次函数关系y=-x+62（1≤x≤12且为整数），而去年的月销量p（棵）与月份x之间成某种函数关系，其中四个月的销售情况如下表：

月份x	1月	2月	3月	6月
月销量p（单位：棵）	500	600	700	1000

（1）判断p与x满足我们学过的哪种函数关系？求出函数关系式并验证你的判断．
（2）求该种苗在去年哪个月的销售额最大？最大为多少元？
（3）由于气候等条件的影响，今年1月该种苗的销量比去年12月下降25%．若将今年1月售出的种苗全部进行移栽，则移栽当年的存活率为（1-n%），且平均每株已成活的种苗可吸碳1.6千克，随着该种苗对环境的适应和生长，预计今年成活的种苗明年的成活率为（1-0.2n%），每株已成活种苗的吸碳能力增加0.5n%，未成活种苗在其成活期间吸碳量忽略不计的情况下，预计明年的吸碳量比今年提高2%，求n的整数值．
（参考数据：（

）

查看答案和解析>>

科目：初中数学 来源：不详 题型：解答题

十二五期间，重庆将继续建设“五个重庆”，并以“民生”作为政府工作的首要目标，为尽快缩短城乡差距，在“两翼”地区实施万元增收计划，学农的大学毕业生小王自主创业，在政府的帮助下，引进一种种苗，这种种苗既可以用来观赏，同时还能很好吸收二氧化碳，用来改变空气质量，因此有很好的市场前景．去年销售的这种种苗每棵的售价y（元）与月份x之间满足一次函数关系y=-x+62（1≤x≤12且为整数），而去年的月销量p（棵）与月份x之间成某种函数关系，其中四个月的销售情况如下表：

月份x	1月	2月	3月	6月
月销量p（单位：棵）	500	600	700	1000

（1）判断p与x满足我们学过的哪种函数关系？求出函数关系式并验证你的判断．
（2）求该种苗在去年哪个月的销售额最大？最大为多少元？
（3）由于气候等条件的影响，今年1月该种苗的销量比去年12月下降25%．若将今年1月售出的种苗全部进行移栽，则移栽当年的存活率为（1-n%），且平均每株已成活的种苗可吸碳1.6千克，随着该种苗对环境的适应和生长，预计今年成活的种苗明年的成活率为（1-0.2n%），每株已成活种苗的吸碳能力增加0.5n%，未成活种苗在其成活期间吸碳量忽略不计的情况下，预计明年的吸碳量比今年提高2%，求n的整数值．
（参考数据：（

203

≈14.248，

205

≈14.318，

206

≈14.353）

查看答案和解析>>

练习册

高中

初中

小学