练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
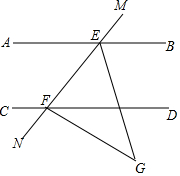
    8．如图，AB∥CD，GE=GF，∠NFG=110°，EG平分∠BEF，求∠DFG的度数．

    分析 先根据等腰三角形的性质，得到∠EFG=70°=∠FEG，再根据EG平分∠BEF，即可得出∠BEM=40°，再根据AB∥CD，可得∠DFE=∠BEM=40°，最后根据∠DFG=180°-∠DFE-∠NFG进行计算即可．

    解答 解：∵GE=GF，∠NFG=110°，
    ∴∠EFG=70°=∠FEG，
    又∵EG平分∠BEF，
    ∴∠BEF=2∠FEG=140°，
    ∴∠BEM=40°，
    ∵AB∥CD，
    ∴∠DFE=∠BEM=40°，
    ∴∠DFG=180°-∠DFE-∠NFG=180°-40°-110°=30°．

    点评 本题主要考查了平行线的性质，角平分线的定义的运用，解题时注意：两直线平行，同位角相等．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    18．如图，已知直线m⊥n，在某平面直角坐标系中，x轴∥直线m，y轴∥直线n，点A、B的坐标分别为（-4，2），（2，-4），点A，O4，B在同一条直线上，则坐标原点为（　　）
    A．O1B．O2C．O3D．O4

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．阅读下列材料：
           近几年，微信红包成为了各种节日甚至是日常生活中表达情感的一种方式．
           据调查：2014年除夕微信红包收发总量为0.16亿个，而2015年的除夕，微信红包的收发总量比上一年除夕增加了60多倍，到达了10.1亿个．2015年的中秋节微信红包的收发总量更是达到了22亿个，其收发红包用户的年龄群体分布大致如图1所示．
           2016年的除夕，微信红包的收发总量为上一年除夕的8倍，初一的凌晨零时06分达到了微信红包收发的最高峰，峰值为每秒40.9万个．
           2017年除夕，微信用户总共收发142亿个红包，创下新高，24时前后，微信红包祝福达到峰值，每秒收发达到76万个．

    根据以上材料解答下列问题：
    （1）图1中，“1～17岁”与“其他”这两个年龄群体所对应扇形的圆心角度数相等，则“1～17岁”年龄群体所占百分比m=6%，“41～50岁”年龄群体所占百分比n=5%；
    （2）将图2中的折线图补充完整，并在图中标明相应数据；
    （3）根据图2提供的信息，预估2018年除夕微信红包收发总量约60亿个，你的预估理由是2016到2017年增幅大体相当．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    16．下列方程为一元一次方程的是（　　）
    A．x+4=4-x2B．x+y=-3xC．$\frac{1}{2x+3}=1$D．5-$\frac{1}{3}x=\frac{2}{3}x$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．解方程（组）：
    （1）2（x+1）=-3（x-4）
    （2）$\left\{\begin{array}{l}{2x-y=5}\\{4x+y=7}\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．已知关于x的一元二次方程m2x2+（2m-1）x+1=0有两个不相等的实数根，求m的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

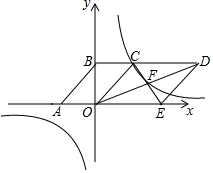    20．如图，已知反比例函数y=$\frac{1-m}{x}$（m为常数）的图象在平面直角坐标系的第一、三象限，且经过?ABCO的顶点C，点A，B的坐标分别为（-2，0），（0，3），若点P是该反比例函数图象上的一点，且OC=OP，则满足条件的位于第三象限内P点坐标为（-3，-2）或（-2，-3）；若该反比例函数图象又经过?COED对角线的交点F，则?COED的面积为18．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    17．某小组参加植树活动，全组学生的植树数量如表所示，则该小组平均每人植树7株．
    植树数量（株）5678
    人数（人）1123

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    18．已知∠α的补角是它的余角度数的3倍，则∠α=45度．

    查看答案和解析>>

    同步练习册答案