练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    14．分解因式：y5-x2y3=y3（y-x）（y+x）．

    分析 先提出公因式y3，再利用平方差公式分解因式即可．

    解答 解：y5-x2y3=y3（y2-x2）=y3（y-x）（y+x），
    故答案为：y3（y-x）（y+x）．

    点评 本题考查了提公因式法和公式法进行分解因式，解决本题的关键是熟记提公因式法和公式法．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

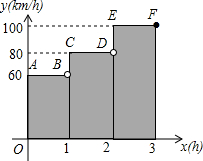    4．一辆汽车在某段路程中的行驶速度v（km/b）与时间t（h）的关系如图线段AB，CD，EF．
    （1）求图中阴影部分的面积．
    （2）说明所求阴影部分的面积的实际意义．
    （3）假设这辆汽车的里程表在汽车行驶这段路程前的读数为2000km，试求行驶这段路程时汽车里程表读数s（km）与时间t（h）的函数关系式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    5．分解因式：-$\frac{1}{4}$x-x3+x2=-x（x-$\frac{1}{2}$）2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

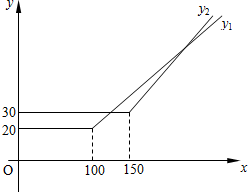    2．某电信公司提供的移动通讯服务的收费标准有两种套餐如表：
    A套餐B套餐
    每月基本服务费a30
    每月免费通话时间100b
    超出每分钟收费0.40.5
    设每月通话时间为x分种，A，B两种套餐每月话费分别为y1，y2元．y1，y2关于x的函数图象如图所示．
    （1）表格中的a=20，b=150；
    （2）通话时间超过每月免费通话时间后，求y1，y2关于x的函数关系式，并写出相应的取值范围；
    （3）已知甲乙两人分别使用A，B两种套餐，他们的通话时间都是t分钟（t＞150），但话费相差5元，求两人的通话时间．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．分解因式：
    （1）m2（a-3）-4（a-3）；
    （2）（x-1）（x-4）+x．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．如图，△ABC中，AB=BC，以AB为一边向外作菱形ABDE，连接DC，EB并延长EB交AC于F，且CB⊥AE于G．
    （1）如图1，若∠EBG=20°，求∠AFE；
    （2）试问线段AE，AF，CF之间的数量关系并证明；
    （3）如图2，延长DB交AC于H，若O为DH的中点，过O作MN∥AC交EF于M，交CD于N，连结NF，若S四边形ABDE=24，BE=6，直接写出BH+NF的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．如图所示，某教学活动小组选定测量山顶铁塔AE的高，他们在30m高的楼CD的底部点D测得塔顶A的仰角为45°，在楼顶C测得塔顶A的仰角为36°52′．若小山高BE=62m，楼的底部D与山脚在同一水平面上，求铁塔的高AE．（参考数据：sin36°52′≈0.60，tan36°52′≈0.75）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

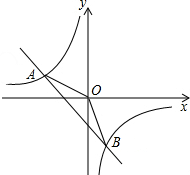    3．如图所示，一次函数y1=kx+b的图象与反比例函数y2=$\frac{m}{x}$的图象交于A（-2，n），B（1，-3）两点．
    （1）试确定上述一次函数和反比例函数的表达式；
    （2）求△AOB的面积；
    （3）根据图象直接写出使y1＜y2的x的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．已知直线y=kx+b与x轴、y轴分别交于A、B两点，与反比例函数交于一象限内的P（$\frac{1}{2}$，n），Q（4，m）两点，且tan∠BOP=$\frac{1}{16}$：
    （1）求反比例函数和直线的函数表达式；
    （2）求△OPQ的面积．

    查看答案和解析>>

    同步练习册答案