
【题目】如图,已知:在平行四边形ABCD中,AB=2,AD=4,∠ABC=60°,E为AD上一点,连接CE,AF∥CE且交BC于点F.
(1)求证:四边形AECF为平行四边形.
(2)证明:△AFB≌△CE D.
(3)DE等于多少时,四边形AECF为菱形.
(4)DE等于多少时,四边形AECF为矩形.

【答案】(1)见解析;(2)见解析;(3)DE=2;(4)DE=1.
【解析】
(1)根据两组对边分别平行的四边形是平行四边形进行证明即可得;
(2)根据ABCD为平行四边形,可得AB=CD, AD=BC,再根据AECF为平行四边形,可得AF=CE,AE=FC,继而可得DE=BF,根据SSS即可证明△AFB≌△CED;
(3)当DE=2时,AECF为菱形,理由:由AB=DC=2,∠ABC=∠EDC=60°可得△EDC为等边三角形,继而可得到AE=EC,根据邻边相等的平行四边形是菱形即可得;
(4)当DE=1时,AECF为矩形,理由:若AECF为矩形则有∠DEC=90°,再根据DC=2,∠D=60°,则可得∠DCE=30°,继而可得DE=1.
(1)∵![]() 为平行四边形,∴
为平行四边形,∴![]() ,即
,即![]() ,
,
又∵![]() (已知),∴
(已知),∴![]() 为平行四边形;
为平行四边形;
(2)∵![]() 为平行四边形,∴
为平行四边形,∴![]() ,
, ![]() ,
,
∵![]() 为平行四边形,∴
为平行四边形,∴![]() ,
,
∴![]() ,
,
在![]() 与
与![]() 中,
中,
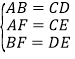 ,
,
∴![]() ;
;
(3)当![]() 时,
时,![]() 为菱形,理由如下:
为菱形,理由如下:
∵![]() ,
,
∴![]() 为等边三角形,
为等边三角形,![]() ,
,![]() ,即:
,即:![]() ,
,
∴平行四边形![]() 为菱形;
为菱形;
(4)当![]() 时,
时,![]() 为矩形,理由如下:
为矩形,理由如下:
若![]() 为矩形得:
为矩形得:![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() .
.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:
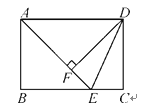
【题目】如图,在长方形ABCD中,点E是BC边上的点,AE=BC,DF⊥AE,垂足为点F,连接DE.
(1)求证:AB=DF;
(2)求证:DE平分∠AEC.
查看答案和解析>>
科目:初中数学 来源: 题型:
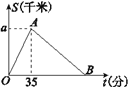
【题目】2016年3月27日“丽水半程马拉松竞赛”在莲都举行,某运动员从起点万地广场西门出发,途经紫金大桥,沿比赛路线跑回终点万地广场西门.设该运动员离开起点的路程S(千米)与跑步时间t(分钟)之间的函数关系如图所示,其中从起点到紫金大桥的平均速度是0.3千米/分,用时35分钟,根据图像提供的信息,解答下列问题:
(1)求图中a的值;
(2)组委会在距离起点2.1千米处设立一个拍摄点C,该运动员从第一次过C点到第二次过C点所用的时间为68分钟.
①求AB所在直线的函数解析式;
②该运动员跑完赛程用时多少分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数的图象经过点A(6,﹣3)和点B(﹣2,5).
(1)求这个一次函数的表达式.
(2)求该函数图象与坐标轴围成的三角形的面积.
(3)判断点C(2,2)是在直线AB的上方(右边)还是下方(左边).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,点 C 是线段 AB 上一点,且 5BC=2AB,D 是 AB 的中点,E 是CB 的中点,(1)若 DE=6,求 AB 的长;(2)求 AD:AC.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知 P是线段 AB上的一点,![]() ,C, D两点从 A, P同时出发,分别以2
,C, D两点从 A, P同时出发,分别以2 ![]() ,1
,1![]() 的速度沿 AB方向运动,当点 D到达终点 B时,点C也停止运动,设AB=
的速度沿 AB方向运动,当点 D到达终点 B时,点C也停止运动,设AB=![]()
![]() ,点 C,D的运动时间为
,点 C,D的运动时间为![]() .
.
(1)用含![]() 和 的代数式表示线段 CP 的长度.
和 的代数式表示线段 CP 的长度.
(2)当 t =5时,![]() ,求线段 AB的长.
,求线段 AB的长.
(3)当 BC-AC=PC时,求 ![]() 的值.
的值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD平分∠BAC,且BD=CD,DE⊥AB于点E,DF⊥AC于点F.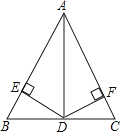
(1)求证:AB=AC;
(2)若AD=2 ![]() ,∠DAC=30°,求AC的长.
,∠DAC=30°,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A的坐标为(﹣2,0),直线y=﹣ ![]() x+3与x轴、y轴分别交于点B和点C,连接AC,顶点为D的抛物线y=ax2+bx+c过A、B、C三点.
x+3与x轴、y轴分别交于点B和点C,连接AC,顶点为D的抛物线y=ax2+bx+c过A、B、C三点. 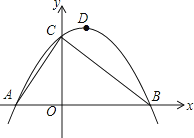
(1)请直接写出B、C两点的坐标,抛物线的解析式及顶点D的坐标;
(2)设抛物线的对称轴DE交线段BC于点E,P是第一象限内抛物线上一点,过点P作x轴的垂线,交线段BC于点F,若四边形DEFP为平行四边形,求点P的坐标;
(3)设点M是线段BC上的一动点,过点M作MN∥AB,交AC于点N,点Q从点B出发,以每秒1个单位长度的速度沿线段BA向点A运动,运动时间为t(秒),当t(秒)为何值时,存在△QMN为等腰直角三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B在线段EF上,点M、N分别是线段EA、BF的中点,EA:AB:BF=1:2:3,若MN=8cm,则线段EF的长是( )
![]()
A. 10 cm B. 11 cm C. 12 cm D. 13 cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com