
数学活动——求重叠部分的面积。
问题情境:数学活动课上,老师出示了一个问题:
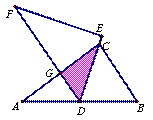
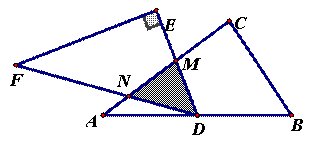
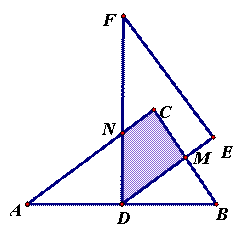
如图,将两块全等的直角三角形纸片△ABC和△DEF叠放在一起,其中∠ACB=∠E=90°,BC=DE=6,AC=FE=8,顶点D与边AB的中点重合,DE经过点C,DF交AC于点G。
求重叠部分(△DCG)的面积。
(1)独立思考:请解答老师提出的问题。
(2)合作交流:“希望”小组受此问题的启发,将△DEF绕点D旋转,使DE⊥AB交AC于点H,DF交AC于点G,如图(2),你能求出重叠部分(△DGH)的面积吗?请写出解答过程。
(3)提出问题:老师要求各小组向“希望”小组学习,将△DEF绕点D旋转,再提出一个求重叠部分面积的问题。“爱心”小组提出的问题是:如图(3),将△DEF绕点D旋转,DE,DF分别交AC于点M,N,使DM=MN求重叠部分(△DMN)的面积、
任务:①请解决“爱心”小组所提出的问题,直接写出△DMN的面积是
②请你仿照以上两个小组,大胆提出一个符合老师要求的问题,并在图中画出图形,标明字母,不必解答(注:也可在图(1)的基础上按顺时针方向旋转)。
【解析】解:∵∠ACB=90°D是AB的中点,
| |
又∵△ABC≌△FDE,∴∠FDE=∠B
∴∠FDE=∠DCB,∴DG∥BC∴∠AGD=∠ACB=90°∴DG⊥AC
又∵DC=DA,∴G是AC的中点,
∴CG=![]() AC=
AC=![]() ×8=4,DG=
×8=4,DG=![]() BC=
BC=![]() ×6=3
×6=3
∴SDCG=![]() ×CG·DG=
×CG·DG=![]() ×4×3=6
×4×3=6
|
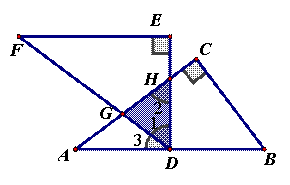
∵△ABC≌△FDE,∴∠B=∠1
∵∠C=90°,ED⊥AB,∴∠A+∠B=90°, ∠A+∠2=90°,
∴∠B=∠2,∴∠1=∠2
∴GH=GD
∵∠A+∠2=90°,∠1+∠3=90°
∴∠A=∠3,∴AG=GD,∴AG=GH
∴点G是AH的中点,
在Rt△ABC中,AB= 10
∵D是AB的中点,∴AD=![]() AB=5
AB=5
在△ADH与△ACB中,∵∠A =∠A,∠ADH=∠ACB=90°,
∴△ADH∽△ACB, ∴![]() =
=![]() ,
,![]() =
=![]() ,∴DH=
,∴DH=![]() ,
,
∴S△DGH=![]() S△ADH=
S△ADH=![]() ×
×![]() ×DH·AD=
×DH·AD=![]() ×
×![]() ×5=
×5=![]()
|

连接BH,∵DE⊥AB,D是AB的中点,∴AH=BH,设AH=x则CH=8-x
在Rt△BCH中,CH2+BC2=BH2,即(8-x)2+36=x2,解得x=
∴S△ABH=AH·BC=![]() ×
×![]() ×6=
×6=![]()
|
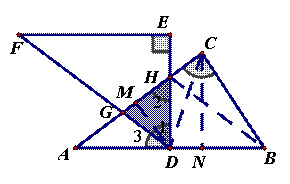
解法三:同解法一,∠1=∠2
连接CD,由(1)知,∠B=∠DCB=∠1,∠1=∠2=∠B=∠DCB,△DGH∽△BDC,
作DM⊥AC于点M,CN⊥AB于点N,∵D是AB的中点,∠ACB=90°
∴CD=AD=BD,∴点M是AC的中点,∴DM=![]() BC=
BC=![]() ×6=3
×6=3
在Rt△ABC中,AB=![]() =10,
=10,![]() AC·BC=
AC·BC=![]() AB·CN,
AB·CN,
∴CN=![]() .
.
∵△DGH∽△BDC, ∴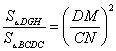 ,
,
∴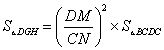 =
=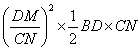
∴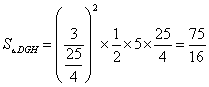
|
|
【答案】①![]()
②注:此题答案不唯一,语言表达清晰、准确得1分,画图正确得1分,重叠部分未涂阴影不扣分。示例:如图,将△DEF绕点D旋转,使DE⊥BC于点M,DF交AC于点N,求重叠部分(四边形DMCN)的面积。


 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
数学活动与思考
我们要学会用数学的眼光看世界——丰富多彩的图形世界。在“图形世界”里,见到许多熟悉的基本图形,感受到图形的平移、翻折、旋转等变化;也发现“图形世界”是由基本图形构成的.可以利用这些变化和基本图形设计出符合要求的图形.
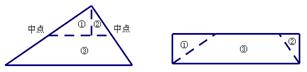 例:直角三角形通过剪切可以拼成一个与该直角三角形面积相等的长方形.方法如图示:
例:直角三角形通过剪切可以拼成一个与该直角三角形面积相等的长方形.方法如图示:
请你用图示的方法解答下列问题:
(1)如图,对一个任意的三角形,设计一种方案,将它分成若干块,再拼成一个与原三角形面积相等的长方形;
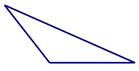
(2)如图,对一个任意的四边形,设计一种方案,将它分成若干块,再拼成一个与原四边形面积相等的长方形;

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com