
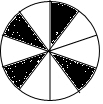
 如图所示的圆形纸板被等分成10个扇形挂在墙上,玩飞镖游戏(每次飞镖均落在纸板上),则飞镖落在阴影区域的概率是$\frac{2}{5}$.
如图所示的圆形纸板被等分成10个扇形挂在墙上,玩飞镖游戏(每次飞镖均落在纸板上),则飞镖落在阴影区域的概率是$\frac{2}{5}$. 科目:初中数学 来源: 题型:解答题
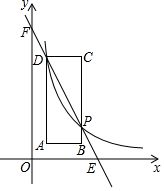 如图,矩形ABCD中,点A(1,1)、B(3,1),C(3,6),反比例函数y=$\frac{m}{x}$(x>0)的图象经过点D,且与BC交于点P.
如图,矩形ABCD中,点A(1,1)、B(3,1),C(3,6),反比例函数y=$\frac{m}{x}$(x>0)的图象经过点D,且与BC交于点P.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
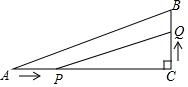 如图,在Rt△ABC中,∠C=90°,AC=6cm,BC=2cm,点P在边AC上,从点A向点C移动,点Q在边CB上,从点C向点B移动.若点P,Q均以1cm/s的速度同时出发,且当一点移动到终点时,另一点也随之停止,连接PQ,则线段PQ的最小值是( )
如图,在Rt△ABC中,∠C=90°,AC=6cm,BC=2cm,点P在边AC上,从点A向点C移动,点Q在边CB上,从点C向点B移动.若点P,Q均以1cm/s的速度同时出发,且当一点移动到终点时,另一点也随之停止,连接PQ,则线段PQ的最小值是( )| A. | 20cm | B. | 18cm | C. | 2$\sqrt{5}$cm | D. | 3$\sqrt{2}$cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
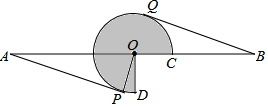 如图,AB=16,O为AB中点,点C在线段OB上(不与点O,B重合),将OC绕点O逆时针旋转270°后得到扇形COD,AP,BQ分别切优弧$\widehat{CD}$于点P,Q,且点P,Q在AB异侧,连接OP.
如图,AB=16,O为AB中点,点C在线段OB上(不与点O,B重合),将OC绕点O逆时针旋转270°后得到扇形COD,AP,BQ分别切优弧$\widehat{CD}$于点P,Q,且点P,Q在AB异侧,连接OP.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 身高/cm | 159 | 160 | 161 | 162 |
| 人数 | 7 | 10 | 9 | 9 |
| A. | 160和160 | B. | 160和160.5 | C. | 160和161 | D. | 161和161 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
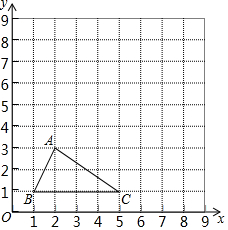 在平面直角坐标系中,△ABC三个顶点的坐标分别为A(2,3),B(1,1),C(5,1).
在平面直角坐标系中,△ABC三个顶点的坐标分别为A(2,3),B(1,1),C(5,1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
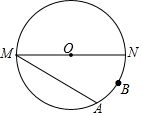 如图,MN是⊙O的直径,MN=4,点A在⊙O上,∠AMN=30°,B为$\widehat{AN}$的中点,P是直径MN上一动点.
如图,MN是⊙O的直径,MN=4,点A在⊙O上,∠AMN=30°,B为$\widehat{AN}$的中点,P是直径MN上一动点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com