
【题目】如图,I是△ABC的内心,∠BAC的平分线与△ABC的外接圆相交于点D,交BC于点E.
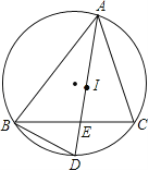
(1)求证:BD=ID;
(2)求证:ID2=DEDA.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
试题(1)连接BI,CI,CD,求证△BCD为等腰三角形,再利用BI为∠ABC平分线,求证△DBI为等腰三角形,利用等量代换即可证明;
(2)证△DBE∽△DAB,得DB2=DEDA,再由(2)得DI2=DEDA.
试题解析:(1)证明:连接BI,CI,CD,
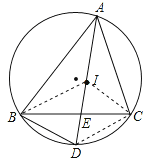
∵I为内心,
∴AI为∠BAC角平分线,
BI为∠ABC平分线,
∴∠ABI=∠CBI,∠BAD=∠DAC,
∵∠BID=∠ABI+∠BAI,
∠CBD=∠DAC=∠BAI,
∴∠BID=∠CBI+∠CBD=∠DBI,
∴△DBI为等腰三角形,
∴DB=DI;
(2)证明:∵∠DBE=∠CAD,∠BAE=∠CAE,
∴∠BAE=∠EBD,
∴△DBE∽△DAB,
∴![]()
∴DB2=DEDA,
又∵DB=DI(已证),
∴DI2=DEDA.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:
【题目】如图,点C是⊙O优弧ACB上的中点,弦AB=6cm,E为OC上任意一点,动点F从点A出发,以每秒1cm的速度沿AB方向响点B匀速运动,若y=AE-EF,则y与动点F的运动时间x(0≤x≤6 )秒的函数关系式为 .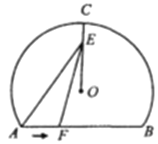
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知线段a=0.3m,b=60cm,c=12dm.
(1)求线段a与线段b的比.
(2)如果线段a、b、c、d成比例,求线段d的长.
(3)b是a和c的比例中项吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中装有仅颜色不同的10个小球,其中红球4个,黑球6个.
(1)先从袋子中取出m(m>1)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A,请完成下列表格;
![]()
(2)先从袋子中取出m个红球,再放入m个一样的黑球并摇匀,随机摸出1个黑球的概率等于![]() ,求m的值.
,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
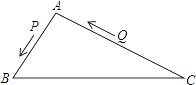
【题目】如图,△ABC中,AB=8厘米,AC=16厘米,点P从A出发,以每秒2厘米的速度向B运动,点Q从C同时出发,以每秒3厘米的速度向A运动,其中一个动点到端点时,另一个动点也相应停止运动,那么,当以A、P、Q为顶点的三角形与△ABC相似时,运动时间是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
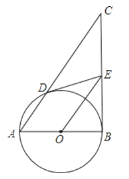
【题目】已知:以Rt△ABC的直角边AB为直径作⊙O,与斜边AC交于点D,过点D作⊙O的切线交BC边于点E.
(1)如图,求证:EB=EC=ED;
(2)试问在线段DC上是否存在点F,满足BC2=4DFDC?若存在,作出点F,并予以证明;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(6分)株洲五桥主桥主孔为拱梁钢构组合体系(如图1),小明暑假旅游时,来到五桥观光,发现拱梁的路面部分有均匀排列着9根支柱,他回家上网查到了拱梁是抛物线,其跨度为20米,拱高(中柱)10米,于是他建立如图2的坐标系,发现可以将余下的8根支柱的高度都算出来了,请你求出中柱左边第二根支柱CD的高度.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+2x+c经过点A(0,3),B(﹣1,0),请解答下列问题:
(1)求抛物线的解析式;
(2)抛物线的顶点为点D,对称轴与x轴交于点E,连接BD,求BD的长.
注:抛物线y=ax2+bx+c(a≠0)的顶点坐标是(﹣![]() ,
,![]() ).
).

查看答案和解析>>
科目:初中数学 来源: 题型:
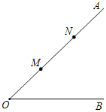
【题目】如图,∠AOB=45°,点M,N在边OA上,OM=3,ON=7,点P是直线OB上的点,要使点P,M,N构成等腰三角形的点P有________个.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com