
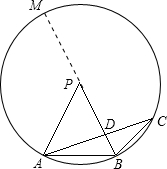
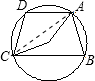
A、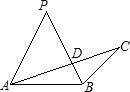 如图,若PA=PB,∠APB=2∠ACB,AC与PB交于点D,且PB=4,PD=3,则AD•DC等于6 | B、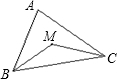 M是△ABC的内心,∠BMC=130°,则∠A的度数为50° | C、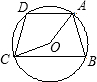 如图,⊙O中,弦AD∥BC,DA=DC,∠AOC=160°,则∠BCO等于80° | D、若一圆锥的轴截面是等边三角形,则其侧面展开图的圆心角是120° |
| 1 |
| 2 |
| 1 |
| 2 |
| nπ2a |
| 180 |


 学业测评一课一测系列答案
学业测评一课一测系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com