
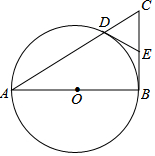
 如图,Rt△ABC中,∠ABC=90°,以AB为直径作⊙O交AC于点D,点E为BC的中点,连接DE.
如图,Rt△ABC中,∠ABC=90°,以AB为直径作⊙O交AC于点D,点E为BC的中点,连接DE.分析 (1)连接DO,DB,由圆周角定理就可以得出∠ADB=90°,可以得出∠CDB=90°,根据E为BC的中点可以得出DE=BE,就有∠EDB=∠EBD,OD=OB可以得出∠ODB=∠OBD,由的等式的性质就可以得出∠ODE=90°就可以得出结论;
(2)由(1)得BC=2DE=6,由BC=2DE求得BC的长,根据AD=$\frac{BD}{tanA}$可得答案.
解答 解:(1)连接DO,DB,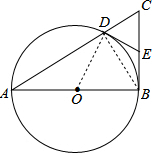
∴OD=OB
∴∠ODB=∠OBD.
∵AB是直径,
∴∠ADB=90°,
∴∠CDB=90°.
∵E为BC的中点,
∴DE为Rt△BCD斜边的中线,
∴DE=BE,
∴∠EDB=∠EBD,
∴∠ODB+∠EDB=∠OBD+∠EBD,
即∠EDO=∠EBO.
∵∠ABC=90°,
∴∠EDO=90°.
∴DE为⊙O的切线;
(2)由(1)知BC=2DE=6,
又∵∠BAC=30°,
∴∠C=60°,
∴BD=BCsinC=6×$\frac{\sqrt{3}}{2}$=3$\sqrt{3}$,
∴AD=$\frac{BD}{tanA}$=$\frac{3\sqrt{3}}{\frac{\sqrt{3}}{3}}$=9.
点评 本题主要考查了切线的判定、圆周角定理及其推论、三角函数的应用等几何知识点及其应用问题;熟练掌握切线的判定方法是解本题的关键.


科目:初中数学 来源: 题型:选择题
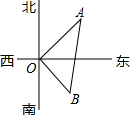 如图,在水塔O的东北方向32m处有一抽水站A,在水塔的东南方向24m处有一建筑工地B,在AB间建一条直水管,则水管的长为( )
如图,在水塔O的东北方向32m处有一抽水站A,在水塔的东南方向24m处有一建筑工地B,在AB间建一条直水管,则水管的长为( )| A. | 45m | B. | 40m | C. | 50m | D. | 56m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
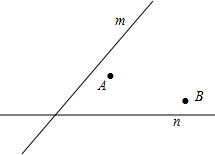 如图,移动公司要在S区修建一座信号发射塔,按照设计要求,发射塔到两个城镇A、B的距离相等,到两条高速公路m和n的距离也相等,请用尺规作图法作出发射塔P的位置.(保留作图痕迹)
如图,移动公司要在S区修建一座信号发射塔,按照设计要求,发射塔到两个城镇A、B的距离相等,到两条高速公路m和n的距离也相等,请用尺规作图法作出发射塔P的位置.(保留作图痕迹)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 |
| -5 | +7 | -9 | +10 | +6 | -5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5 | B. | 10 | C. | 10$\sqrt{2}$ | D. | 5$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
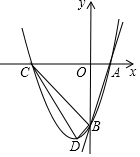 如图,已知直线y=3x-3分别交x轴,y轴于A,B两点,抛物线y=x2+bx+c经过A,B两点,点C是抛物线与x轴的另一个交点(与点A不重合),点D是抛物线的顶点,请解答下列问题.
如图,已知直线y=3x-3分别交x轴,y轴于A,B两点,抛物线y=x2+bx+c经过A,B两点,点C是抛物线与x轴的另一个交点(与点A不重合),点D是抛物线的顶点,请解答下列问题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
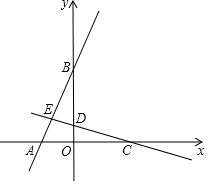 如图,在平面直角坐标系中,直线y=mx+4与x,y轴分别交于A,B两点,直线y=-$\frac{1}{3}$x+n与x,y轴分别交于C,D两点,点E(-$\frac{9}{7}$,$\frac{10}{7}$)是这两条直线的交点.
如图,在平面直角坐标系中,直线y=mx+4与x,y轴分别交于A,B两点,直线y=-$\frac{1}{3}$x+n与x,y轴分别交于C,D两点,点E(-$\frac{9}{7}$,$\frac{10}{7}$)是这两条直线的交点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
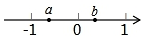 有理数a,b在数轴上对应的位置如图所示,那么代数式$\frac{|a+1|}{a+1}$-$\frac{|a|}{a}$+$\frac{b-a}{|a-b|}$-$\frac{1-b}{|b-1|}$的值是2.
有理数a,b在数轴上对应的位置如图所示,那么代数式$\frac{|a+1|}{a+1}$-$\frac{|a|}{a}$+$\frac{b-a}{|a-b|}$-$\frac{1-b}{|b-1|}$的值是2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com