
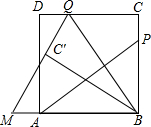
 如图,P为正方形ABCD的边BC上一动点(P与B、C不重合),连接AP,过点B作BQ⊥AP交CD于点Q,将△BQC沿BQ所在的直线对折得到△BQC′,延长QC′交BA的延长线于点M.
如图,P为正方形ABCD的边BC上一动点(P与B、C不重合),连接AP,过点B作BQ⊥AP交CD于点Q,将△BQC沿BQ所在的直线对折得到△BQC′,延长QC′交BA的延长线于点M.分析 (1)要证AP=BQ,只需证△PBA≌△QCB即可;
(2)过点Q作QH⊥AB于H,如图.易得QH=BC=AB=3,BP=2,PC=1,然后运用勾股定理可求得AP(即BQ)=$\sqrt{13}$,BH=2.易得DC∥AB,从而有∠CQB=∠QBA.由折叠可得∠C′QB=∠CQB,即可得到∠QBA=∠C′QB,即可得到MQ=MB.设QM=x,则有MB=x,MH=x-2.在Rt△MHQ中运用勾股定理就可解决问题;
(3)过点Q作QH⊥AB于H,如图,同(2)的方法求出QM的长,就可得到AM的长.
解答 解:(1)AP=BQ.
理由:∵四边形ABCD是正方形,
∴AB=BC,∠ABC=∠C=90°,
∴∠ABQ+∠CBQ=90°.
∵BQ⊥AP,∴∠PAB+∠QBA=90°,
∴∠PAB=∠CBQ.
在△PBA和△QCB中,
$\left\{\begin{array}{l}{∠PAB=∠CBQ}\\{AB=BC}\\{∠ABP=∠BCQ}\end{array}\right.$,
∴△PBA≌△QCB,
∴AP=BQ;
(2)过点Q作QH⊥AB于H,如图.
∵四边形ABCD是正方形,
∴QH=BC=AB=3.
∵BP=2PC,
∴BP=2,PC=1,
∴BQ=AP=$\sqrt{A{B}^{2}+P{B}^{2}}$=$\sqrt{{3}^{2}+{2}^{2}}$=$\sqrt{13}$,
∴BH=$\sqrt{B{Q}^{2}-Q{H}^{2}}$=$\sqrt{13-9}$=2.
∵四边形ABCD是正方形,
∴DC∥AB,
∴∠CQB=∠QBA.
由折叠可得∠C′QB=∠CQB,
∴∠QBA=∠C′QB,
∴MQ=MB.
设QM=x,则有MB=x,MH=x-2.
在Rt△MHQ中,
根据勾股定理可得x2=(x-2)2+32,
解得x=$\frac{13}{4}$.
∴QM的长为$\frac{13}{4}$;
(3)过点Q作QH⊥AB于H,如图.
∵四边形ABCD是正方形,BP=m,PC=n,
∴QH=BC=AB=m+n.
∴BQ2=AP2=AB2+PB2,
∴BH2=BQ2-QH2=AB2+PB2-AB2=PB2,
∴BH=PB=m.
设QM=x,则有MB=QM=x,MH=x-m.
在Rt△MHQ中,
根据勾股定理可得x2=(x-m)2+(m+n)2,
解得x=m+n+$\frac{{n}^{2}}{2m}$,
∴AM=MB-AB=m+n+$\frac{{n}^{2}}{2m}$-m-n=$\frac{{n}^{2}}{2m}$.
∴AM的长为$\frac{{n}^{2}}{2m}$.
点评 本题主要考查了正方形的性质、全等三角形的判定与性质、勾股定理、轴对称的性质等知识,设未知数,然后运用勾股定理建立方程,是求线段长度常用的方法,应熟练掌握.


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:解答题
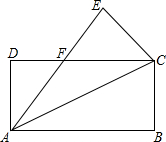 根据要求将下面题目改编成一道新题:如图,将矩形ABCD沿对角线AC折叠,点B落在E处,AE交DC于点F,求证:折叠后的重叠部分(即△FAC)是等腰三角形
根据要求将下面题目改编成一道新题:如图,将矩形ABCD沿对角线AC折叠,点B落在E处,AE交DC于点F,求证:折叠后的重叠部分(即△FAC)是等腰三角形查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com