练习册

  • 练习册
  • 试题
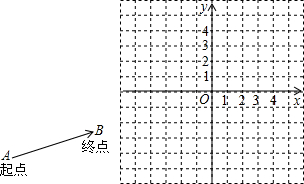
    精英家教网 > 初中数学 > 题目详情

    如下图在4×4的正方形方格中，△ABC的顶点A、B、C分别在小正方形的顶点上，请在图中画△A1B1C1，使△A1B1C1∽△ABC(相似比不为1)，且点A1、B1、C1都分别在小正方形的顶点上．

    答案：
    提示：

    将各边扩大2倍．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：阅读理解

    先阅读短文，再解答短文后面的问题．
    规定了方向的线段称为有向线段．比如，对于线段AB，规定以A为起点，B为终点，便可得到一条从A到B的有向线段．为强调其方向，我们在其终点B处画上箭头（如下图-1）．以A为起点，B为终点的有向线段记为
    AB
    （起点字母A写在前面，终点字母B写在后面）．线段AB的长度叫做有向线AB的长度（或模），记为|
    AB
    |．显然，有向线段
    AB
    和有向线段
    BA
    长度相同．方向不同，它们不是同一条有向线段．
    对于同一平面内的有向线段，我们可以在该平面建立直角坐标系进行研究（一般情况，直角坐标系的单位长度与有向线段的单位长度相同）．比如，以坐标原点O（0，0）为起点，P（3，0）为终点的有向线段
    OP
    ，其方向与x轴正方向相同，长度（或模）是|
    OP
    |=3．
    问题：
    （1）在如图所示的平面直角坐标系中画出
    OA
    有向线段，使得
    OA
    =3
    		2
    ，
    OA
    与x轴正半轴的夹角是45°，且与y轴的负半轴的夹角是45°；
    （2）若有向线段
    OB
    的终点B的坐标为（3，
    		3
    ），试求出它的模及它与x轴正半轴的夹角；
    （3）若点M、A、P在同一直线上，|
    MA
    |+|
    AP
    |=|
    MP
    |    成立吗？试画出示意图加以说明．（示意图可以不画在平面直角坐标系中）
    精英家教网

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    27、（任选一题，若两题都选按得分最少的题记分）
    （1）甲乙两辆汽车在一条公路上匀速行驶，为了确定汽车的位置，我们用数轴Ox表示这条公路，原点O为零千米路标（如图1），并作如下约定：
    ①速度v＞0，表示汽车向数轴正方向行驶；速度v＜0，表示汽车向数轴负方向行驶；速度v=0，表示汽车静止．
    ②汽车位置在数轴上的坐标s＞0，表示汽车位于零千米路标的右侧；汽车位置在数轴上的坐标s＜0，表示汽车位于零千米路标的左侧；汽车位置在数轴上的坐标s=0，表示汽车恰好位于零千米路标处．
    遵照上述约定，将这两辆汽车在公路上匀速行驶的情况，以一次函数图象的形式画在了同一直角坐标系中，如图2，请解答下列问题：
    ①就这两个一次函数图象所反映的两汽车在这条公路上行驶的状况填写如下的表格．

    ②甲乙两车能否相遇？如能相遇，求相遇时的时刻及在公路上的位置；如不能相遇，请说明理由．

    （2）在一次蜡烛燃烧实验中，甲、乙两根蜡烛燃烧时剩余的高度y（cm）与燃烧时间x（分钟）的关系如下图所示，根据图象提供的信息解答下列问题：
    ①指出两根蜡烛燃烧前的高度；
    ②分别求出甲、乙两根蜡烛燃烧时y与x之间的函数关系式；
    ③x为何值时，甲、乙两根蜡烛在燃烧过程中的高度相等．

    查看答案和解析>>

    科目：初中数学 来源：2006年吉林省长春市初中毕业生学业考试数学试题 题型：044

    如下图，正方形ABCD的顶点A，B的坐标分别为(0，10)，(8，4)，顶点C，D在第一象限．点P从点A出发，沿正方形按逆时针方向匀速运动，同时，点Q从点E(4，0)出发，沿x轴正方向以相同速度运动．当点P到达点C时，P，Q两点同时停止运动，设运动的时间为t秒．

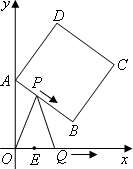
    (1)求正方形ABCD的边长．

    (2)当点P在AB边上运动时，△OPQ的面积S(平方单位)与时间t(秒)之间的函数图象为抛物线的一部分(如图所示)，求P，Q两点的运动速度．

    (3)求(2)中面积S(平方单位)与时间t(秒)的函数关系式及面积S取最大值时点P的坐标．

    (4)若点P，Q保持(2)中的速度不变，则点P沿着AB边运动时，∠OPQ的大小随着时间t的增大而增大；沿着BC边运动时，∠OPQ的大小随着时间t的增大而减小．当点P沿着这两边运动时，使∠OPQ＝90°的点P有________个．

    (抛物线y＝ax2＋bx＋c(a≠0)的顶点坐标是．)

    查看答案和解析>>

    科目：初中数学 来源：湖南省郴州市2011年中考数学试题 题型：059

    已知：如下图，等腰梯形ABCD的边BC在x轴上，点A在y轴的正方向上，A(0，6)，D(4，6)，且AB＝．

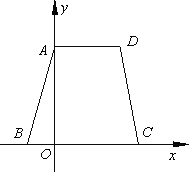
    (1)求点B的坐标；

    (2)求经过A、B、D三点的抛物线的解析式；

    (3)在(2)中所求的抛物线上是否存在一点P，使得？若存在，请求出该点坐标，若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源：同步题 题型：解答题

    点P是x轴正半轴上的一个动点，过点P作x轴的垂线PA交双曲线上于点A，连接OA。
    （1）如下图（1），当点P在x轴的正方向上运动时，Rt△AOP的面积大小是否变化？若不变，请求出Rt△AOP的面积；若改变，试说明理由；
    （2）如下图（2），在x轴上的点P的右侧有一点D，过点D作x轴的垂线交双曲线于点B，连接BO交AP 于点G设△AOP的面积为S1，梯形BCPD的面积为S2，则S1与S2的大小关系是S1（    ）S2。（选填或）
    （3）如下图（3），AO的延长线与双曲线的另一个交点是点F，FH⊥x轴，垂足为 H，连接AH，PF，试证明四边形APFH的面积为一常数。

    查看答案和解析>>

    同步练习册答案