
дкЦНУцжБНЧзјБъЯЕxOyжаЃЌвбжЊХзЮяЯп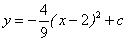 гыxжсНЛгкAЁЂBСНЕуЃЈЕуAдкЕуBЕФзѓВрЃЉЃЌНЛyжсЕФе§АыжсгкЕуCЃЌЦфЖЅЕуЮЊMЃЌMHЁЭxжсгкЕуHЃЌMAНЛyжсгкЕуNЃЌsinЁЯMOHЃН
гыxжсНЛгкAЁЂBСНЕуЃЈЕуAдкЕуBЕФзѓВрЃЉЃЌНЛyжсЕФе§АыжсгкЕуCЃЌЦфЖЅЕуЮЊMЃЌMHЁЭxжсгкЕуHЃЌMAНЛyжсгкЕуNЃЌsinЁЯMOHЃН .
.
ЃЈ1ЃЉЧѓДЫХзЮяЯпЕФКЏЪ§БэДяЪНЃЛ
ЃЈ2ЃЉЙ§HЕФжБЯпгыyжсЯрНЛгкЕуPЃЌЙ§OЃЌMСНЕузїжБЯпPHЕФДЙЯпЃЌДЙзуЗжБ№ЮЊEЃЌFЃЌШє  ЃН
ЃН ЪБЃЌЧѓЕуPЕФзјБъЃЛ
ЪБЃЌЧѓЕуPЕФзјБъЃЛ
ЃЈ3ЃЉНЋЃЈ1ЃЉжаЕФХзЮяЯпбиyжселЕўЃЌЪЙЕуAТфдкЕуDДІЃЌСЌНгMDЃЌQЮЊЃЈ1ЃЉжаЕФХзЮяЯпЩЯЕФвЛЖЏЕуЃЌжБЯпNQНЛxжсгкЕуGЃЌЕБQЕудкХзЮяЯпЩЯдЫЖЏЪБЃЌЪЧЗёДцдкЕуQЃЌЪЙЁїANG гыЁїADMЯрЫЦЃПШєДцдкЃЌЧѓГіЫљгаЗћКЯЬѕМўЕФжБЯпQGЕФНтЮіЪНЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ
 |
НтЃКЃЈ1ЃЉЁп MЮЊХзЮяЯп ЕФЖЅЕуЃЌ
ЕФЖЅЕуЃЌ
ЁрMЃЈ2ЃЌcЃЉЃЎЁрOHЃН2ЃЌMHЃН|c|ЃЎЁпa<0ЃЌЧвХзЮяЯпгыxжсгаНЛЕуЃЌЁрcЃО0ЃЌЁрMHЃНcЃЎ
ЁпsinЁЯMOHЃН ЃЌЁр
ЃЌЁр ЃЎЁрOMЃН
ЃЎЁрOMЃН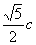 ЃЌЁп
ЃЌЁп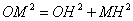 ЃЌЁрMHЃНcЃН4ЃЎЁрMЃЈ2ЃЌ4ЃЉЃЎЁрХзЮяЯпЕФКЏЪ§БэДяЪНЮЊЃК
ЃЌЁрMHЃНcЃН4ЃЎЁрMЃЈ2ЃЌ4ЃЉЃЎЁрХзЮяЯпЕФКЏЪ§БэДяЪНЮЊЃК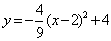 ЃЎ-----------4Зж
ЃЎ-----------4Зж
ЃЈ2ЃЉШчЭМ1ЃЌЁпOEЁЭPHЃЌMFЁЭPHЃЌMHЁЭOHЃЎ
ЁрЁЯEHOЃНЁЯFMHЃЌЁЯOEHЃНЁЯHFMЃЎЁрЁїOEHЁзЁїHFMЃЎ----------2Зж
Ёр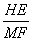 ЃН
ЃН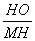 ЃН
ЃН ЃЎЁп
ЃЎЁп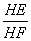 ЃН
ЃН ЃЌЁрMFЃНHFЃЎ
ЃЌЁрMFЃНHFЃЎ
ЁрЁЯOHPЃНЁЯFHMЃН45ЁуЃЎЁрOPЃНOHЃН2ЃЌЁрPЃЈ0ЃЌ2ЃЉЃЎ
ШчЭМ2ЃЌЭЌРэПЩЕУЃЌPЃЈ0ЃЌЉ2ЃЉЃЎ-------------------------------------------2Зж


ЃЈ3ЃЉЁпAЃЈ-1ЃЌ0ЃЉЃЌЁрDЃЈ1ЃЌ0ЃЉЃЎ
ЁпMЃЈ2ЃЌ4ЃЉЃЌDЃЈ1ЃЌ0ЃЉЃЌЁрMDЃК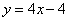 ЃЎЁпONЁЮMHЃЌЁрЁїAONЁзЁїAHMЃЌЁр
ЃЎЁпONЁЮMHЃЌЁрЁїAONЁзЁїAHMЃЌЁр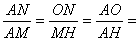
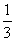 ЃЌЁрANЃН
ЃЌЁрANЃН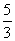 ЃЌONЃН
ЃЌONЃН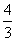 ЃЌNЃЈ0ЃЌ
ЃЌNЃЈ0ЃЌ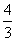 ЃЉЃЎ
ЃЉЃЎ
ШчЭМ3ЃЌШєЁїANG Ёз ЁїAMDЃЌПЩЕУNGЁЮMDЃЌЁрQGЃК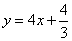 ЃЎ--------2Зж
ЃЎ--------2Зж
ШчЭМ4ЃЌШєЁїANG Ёз ЁїADMЃЌПЩЕУЃЌ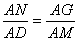 ЃЎ
ЃЎ
ЁрAGЃН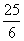 ЃЌЁрGЃЈ
ЃЌЁрGЃЈ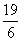 ЃЌ0ЃЉЃЌЁрQGЃК
ЃЌ0ЃЉЃЌЁрQGЃК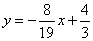 ЃЛ
ЃЛ
злЩЯЫљЪіЃЌЗћКЯЬѕМўЕФЫљгажБЯпQGЕФНтЮіЪНЮЊЃК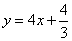 Лђ
Лђ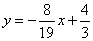 ЃЎ---2Зж
ЃЎ---2Зж
 |  |


 ПкЫуФмЪжЯЕСаД№АИ
ПкЫуФмЪжЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
вЛДЮКЏЪ§y=(k-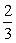 )xЃ3k+10ЃЈkЮЊХМЪ§ЃЉЕФЭМЯѓОЙ§ЕквЛЁЂЖўЁЂШ§ЯѓЯоЃЌгыxжсЁЂyжсЗжБ№НЛгкAЁЂBСНЕуЃЌЙ§ЕуBзївЛжБЯпгызјБъжсЮЇГЩЕФШ§НЧаЮУцЛ§ЮЊ2ЃЌНЛxжсгкЕуC.
)xЃ3k+10ЃЈkЮЊХМЪ§ЃЉЕФЭМЯѓОЙ§ЕквЛЁЂЖўЁЂШ§ЯѓЯоЃЌгыxжсЁЂyжсЗжБ№НЛгкAЁЂBСНЕуЃЌЙ§ЕуBзївЛжБЯпгызјБъжсЮЇГЩЕФШ§НЧаЮУцЛ§ЮЊ2ЃЌНЛxжсгкЕуC.
ЃЈ1ЃЉЧѓkЕФжЕЃЛ
ЃЈ2ЃЉШєвЛХзЮяЯпОЙ§ЕуAЁЂBЁЂCШ§ЕуЃЌЧѓДЫХзЮяЯпЕФНтЮіЪНЁЃ
ЃЈ3ЃЉЕБХзЮяЯпПЊПкЯђЩЯЪБЙ§AЁЂBЁЂCШ§ЕузїЁїABCЃЌЧѓtanЁЯABCЕФжЕЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
вбжЊЃЌдкЭЌвЛжБНЧзјБъЯЕжаЃЌЗДБШР§КЏЪ§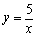 гыЖўДЮКЏЪ§
гыЖўДЮКЏЪ§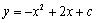 ЕФЭМЯёНЛгкЕу
ЕФЭМЯёНЛгкЕу ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓ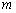 ЁЂ
ЁЂ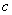 ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉЧѓЖўДЮКЏЪ§ЭМЯёЕФЖдГЦжсКЭЖЅЕузјБъ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
вЛДЮКЏЪ§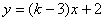 ЃЌШє
ЃЌШє Ыц
Ыц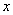 ЕФдіДѓЖјдіДѓЃЌдђ
ЕФдіДѓЖјдіДѓЃЌдђ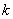 ЕФжЕПЩвдЪЧЃЈ ЃЉ
ЕФжЕПЩвдЪЧЃЈ ЃЉ
ЃЈAЃЉ1 ЃЈBЃЉ2 ЃЈCЃЉ3 ЃЈDЃЉ4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
вбжЊЩШаЮЕФдВаФНЧЮЊ60ЁуЃЌАыОЖЮЊ1ЃЌдђЩШаЮЕФЛЁГЄЮЊЃЈЁЁЁЁЃЉ
| ЁЁ | AЃЎ |
| BЃЎ | Іа | CЃЎ |
| DЃЎ |
|
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЮЊИФЩЦЩњЬЌЛЗОГЃЌЗРжЙЫЎЭССїЪЇЃЌФГДхМЦЛЎдкНККЕЬЦТжжжВАзбюЪїЃЌЯжМзЁЂввСНМвСжГЁгыЯрЭЌЕФАзбюЪїУчПЩЙЉбЁдёЃЌЦфОпЬхЯњЪлЗНАИШчЯТЃК
| МзСжГЁ | ввСжГЁ | ||
| ЙКЪїУчЪ§СП | ЯњЪлЕЅМл | ЙКЪїУчЪ§СП | ЯњЪлЕЅМл |
| ВЛГЌЙ§1000ПУЪБ | 4дЊ/ПУ | ВЛГЌЙ§2000ПУЪБ | 4дЊ/ПУ |
| ГЌЙ§1000ПУЕФВПЗж | 3.8дЊ/ПУ | ГЌЙ§2000ПУЕФВПЗж | 3.6дЊ/ПУ |
ЩшЙКТђАзбюЪїУчxПУЃЌЕНСНМвСжГЁЙКТђЫљашЗбгУЗжБ№ЮЊyМзЃЈдЊЃЉЁЂyввЃЈдЊЃЉЃЎ
ЃЈ1ЃЉИУДхашвЊЙКТђ1500ПУАзбюЪїУчЃЌШєЖМдкМзСжГЁЙКТђЫљашЗбгУЮЊЁЁ ЁЁдЊЃЌШєЖМдкввСжГЁЙКТђЫљашЗбгУЮЊЁЁ дЊЃЛ
ЃЈ2ЃЉЗжБ№ЧѓГіyМзЁЂyввгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ3ЃЉШчЙћФуЪЧИУДхЕФИКд№ШЫЃЌгІИУбЁдёЕНФФМвСжГЁЙКТђЪїУчКЯЫуЃЌЮЊЪВУДЃП
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com