
【题目】解下列方程:
(1)x(x+4)=﹣3(x+4);
(2)(2x+1)(x﹣3)=﹣6.
【答案】
(1)解:(1)x(x+4)=﹣3(x+4),
x(x+4)+3(x+4)=0,
(x+4)(x+3)=0,
x+4=0,x+3=0,
x1=﹣4,x2=﹣3
(2)解:(2x+1)(x﹣3)=﹣6,
整理得:2x2﹣5x+3=0,
(2x﹣3)(x﹣1)=0,
2x﹣3=0,x﹣1=0,
x1= ![]() ,x2=1
,x2=1
【解析】(1)移项后分解因式,即可得出两个一元一次方程,求出方程的解即可;(2)整理后分解因式,即可得出两个一元一次方程,求出方程的解即可.
【考点精析】利用因式分解法对题目进行判断即可得到答案,需要熟知已知未知先分离,因式分解是其次.调整系数等互反,和差积套恒等式.完全平方等常数,间接配方显优势.


科目:初中数学 来源: 题型:
【题目】如图,在边长为1的正方形中,以各顶点为圆心,对角线的长的一半为半径在正方形内画弧,则图中阴影部分的面积为( ) 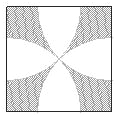
A.2-![]() π
π
B.![]() π
π
C.![]() -1
-1
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,2,3分别以△ABC的AB和AC为边向△ABC外作正三角形(等边三角形)、正四边形(正方形)、正五边形,BE和CD相交于点O.
(1)在图1中,求证:△ABE≌△ADC.
(2)由(1)证得△ABE≌△ADC,由此可推得在图1中∠BOC=120°,请你探索在图2中,∠BOC的度数,并说明理由或写出证明过程.
(3)填空:在上述(1)(2)的基础上可得在图3中∠BOC=(填写度数).
(4)由此推广到一般情形(如图4),分别以△ABC的AB和AC为边向△ABC外作正n边形,BE和CD仍相交于点O,猜想得∠BOC的度数为(用含n的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出:如图(1),在边长为a(a>2)的正方形ABCD各边上分别截取AE=BF=CG=DH=1,当∠AFQ=∠BGM=∠CHN=∠DEP=45°时,求S正方形MNPQ . 问题探究:分别延长QE,MF,NG,PH,交FA,GB,HC,ED的延长线于点R,S,T,W,可得△RQF,△SMG,△TNH,△WPE是四个全等的等腰直角三角形(如图(2)).
(1)若将上述四个等腰三角形拼成一个新的正方形(无缝隙,不重叠),则新正方形的边长为;这个新正方形与原正方形ABCD的面积有何关系;(填“>”,“=”“或<”);通过上述的分析,可以发现S正方形MNPQ与S△FSB之间的关系是:
(2)问题解决:求S正方形MNPQ .
(3)拓展应用:如图(3),在等边△ABC各边上分别截取AD=BE=CF=1,再分别过点D,E,F作BC,AC,AB的垂线,得到等边△PQR,求S△PQR . (请仿照上述探究的方法,在图3的基础上,先画出图形,再解决问题).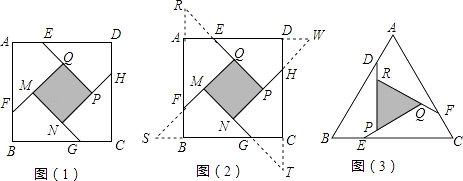
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC,∠C=90°,点D为AB上的一点,以AD为直径的⊙O与BC相切于点E,连接AE. 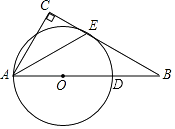
(1)求证:AE平分∠BAC;
(2)若AC=8,OB=18,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】龟兔赛跑,它们从同一地点同时出发,不久兔子就把乌龟远远地甩在后面,于是兔子便得意洋洋地躺在一棵大树下睡起觉来.乌龟一直在坚持不懈、持之以恒地向终点跑着,兔子一觉醒来,看见乌龟快接近终点了,这才慌忙追赶上去,但最终输给了乌龟.下列图象中能大致反映龟兔行走的路程S随时间t变化情况的是( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图③所示,图象过点(﹣1,0),对称轴为直线x=2,则下 列结论中正确的个数有( ) ①4a+b=0;
②9a+3b+c<0;
③若点A(﹣3,y1),点B(﹣ ![]() ,y2),点C(5,y3)在该函数图象上,则y1<y3<y2;
,y2),点C(5,y3)在该函数图象上,则y1<y3<y2;
④若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2 , 且x1<x2 , 则x1<﹣1<5<x2 . 
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com