
【题目】如图,已知Rt△ABC中,∠ACB=90°,以斜边AB为边向外作正方形ABDE,且正方形的对角线交于点O,连结OC.已知AC=5,OC=6![]() ,则另一直角边BC的长为 .
,则另一直角边BC的长为 .

【答案】4
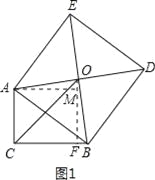
【解析】试题分析:过O作OF垂直于BC,再过A作AM垂直于OF,由四边形ABDE为正方形,得到OA=OB,∠AOB为直角,可得出两个角互余,再由AM垂直于MO,得到△AOM为直角三角形,其两个锐角互余,利用同角的余角相等可得出一对角相等,再由一对直角相等,OA=OB,利用AAS可得出△AOM与△BOF全等,由全等三角形的对应边相等可得出AM=OF,OM=FB,由三个角为直角的四边形为矩形得到ACFM为矩形,根据矩形的对边相等可得出AC=MF,AM=CF,等量代换可得出CF=OF,即△COF为等腰直角三角形,由斜边OC的长,利用勾股定理求出OF与CF的长,根据OF﹣MF求出OM的长,即为FB的长,由CF+FB即可求出BC的长.解法一:如图1所示,过O作OF⊥BC,过A作AM⊥OF,∵四边形ABDE为正方形,∴∠AOB=90°,OA=OB,∴∠AOM+∠BOF=90°,又∠AMO=90°,∴∠AOM+∠OAM=90°,∴∠BOF=∠OAM,在△AOM和△BOF中, 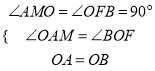 ,∴△AOM≌△BOF(AAS),∴AM=OF,OM=FB,又∠ACB=∠AMF=∠CFM=90°,∴四边形ACFM为矩形,∴AM=CF,AC=MF=5,∴OF=CF,∴△OCF为等腰直角三角形,∵OC=6
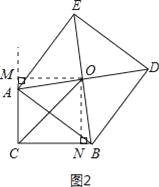
,∴△AOM≌△BOF(AAS),∴AM=OF,OM=FB,又∠ACB=∠AMF=∠CFM=90°,∴四边形ACFM为矩形,∴AM=CF,AC=MF=5,∴OF=CF,∴△OCF为等腰直角三角形,∵OC=6![]() ,∴根据勾股定理得:CF2+OF2=OC2,解得:CF=OF=6,∴FB=OM=OF﹣FM=6﹣5=1,则BC=CF+BF=6+1=7.故答案为:7.解法二:如图2所示,过点O作OM⊥CA,交CA的延长线于点M;过点O作ON⊥BC于点N.易证△OMA≌△ONB,∴OM=ON,MA=NB.∴O点在∠ACB的平分线上,∴△OCM为等腰直角三角形.∵OC=6
,∴根据勾股定理得:CF2+OF2=OC2,解得:CF=OF=6,∴FB=OM=OF﹣FM=6﹣5=1,则BC=CF+BF=6+1=7.故答案为:7.解法二:如图2所示,过点O作OM⊥CA,交CA的延长线于点M;过点O作ON⊥BC于点N.易证△OMA≌△ONB,∴OM=ON,MA=NB.∴O点在∠ACB的平分线上,∴△OCM为等腰直角三角形.∵OC=6![]() ,∴CM=ON=6.∴MA=CM﹣AC=6﹣5=1,∴BC=CN+NB=6+1=7.故答案为:7.
,∴CM=ON=6.∴MA=CM﹣AC=6﹣5=1,∴BC=CN+NB=6+1=7.故答案为:7.


科目:初中数学 来源: 题型:
【题目】小红将笔记本电脑水平放置在桌子上,显示屏OB与底板OA所在的水平线的夹角为120°时,感觉最舒适(如图1),侧面示意图为图2;使用时为了散热,她在底板下垫入散热架ACO′后,电脑转到AO′B′位置(如图3),侧面示意图为图4.已知OA=OB=24cm,O′C⊥OA于点C,O′C=12cm.
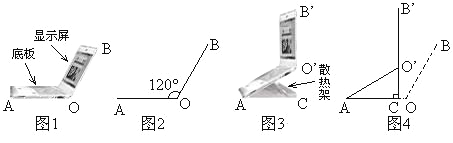
(1)求∠CAO′的度数;
(2)显示屏的顶部B′比原来升高了多少?
(3)如图4,垫入散热架后,要使显示屏O′B′与水平线的夹角仍保持120°,则显示屏O′B′应绕点O′按顺时针方向旋转多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为12,BE=EC,将正方形边CD沿DE折叠到DF,延长EF交AB于G,连接DG,现在有如下4个结论:①△ADG≌△FDG;②GB=2AG;③△GDE∽△BEF;④S△BEF=![]() .在以上4个结论中,正确的有( )
.在以上4个结论中,正确的有( )

A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】市运会举行射击比赛,校射击队从甲、乙、丙、丁四人中选拔一人参赛.在选拔赛中,每人射击10次,计算他们10发成绩的平均数(环)及方差如下表.请你根据表中数据选一人参加比赛,最合适的人选是 .
甲 | 乙 | 丙 | 丁 | |
平均数 | 8.2 | 8.0 | 8.0 | 8.2 |
方差 | 2.1 | 1.8 | 1.6 | 1.4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题8分)已知:如图,△ABC中,D是AB的中点,E是AC上一点,EF∥AB,DF∥BE.
(1)猜想:DF与AE的关系是______.
(2)试说明你猜想的正确性.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com