
| MD |
| DN |
| DP |
| DQ |
| ND |
| BC |
| DP |
| DQ |
| AD |
| AB |
| 2 |
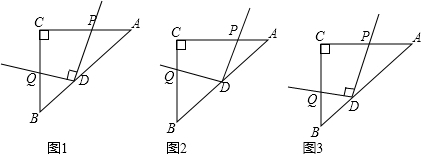
 解:(1)①DP=DQ,
解:(1)①DP=DQ,
|
| MD |
| DN |
| DP |
| DQ |
| AD |
| BD |
| DM |
| DN |
| DP |
| DQ |
| AD |
| BD |
| 2BD |
| BD |
| 2 |
| 1 |
| ND |
| BC |
| DP |
| DQ |
| AD |
| AB |
| DP |
| DQ |
| AN |
| CN |
| AD |
| BD |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
| 3 |
| 9 |
| 2 |
| 9 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2012-2013学年浙江湖州第八中学八年级10月月考数学试卷(带解析) 题型:解答题
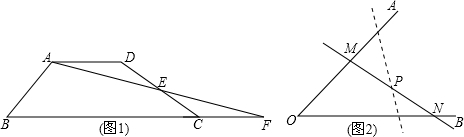
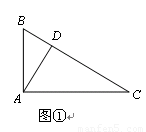
问题情境:如图①,在直角三角形ABC中,∠BAC=90°,AD⊥BC于点D,可知:∠BAD=∠C(不需要证明);
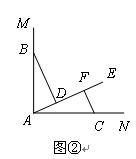
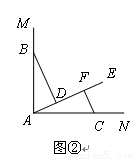
特例探究:如图②,∠MAN=90°,射线AE在这个角的内部,点B、C在∠MAN的边AM、AN上,且AB="AC," CF⊥AE于点F,BD⊥AE于点D.证明:△ABD≌△CAF;
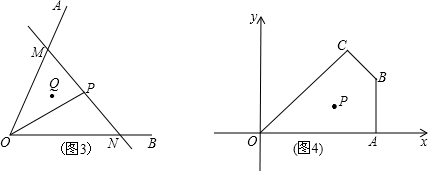
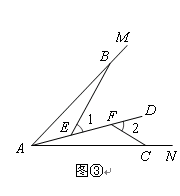
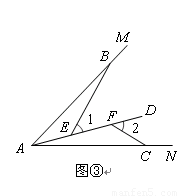
归纳证明:如图③,点BC在∠MAN的边AM、AN上,点EF在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB="AC," ∠1=∠2=∠BAC.求证:△ABE≌△CAF;
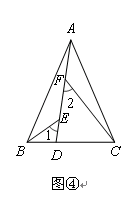
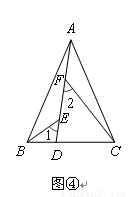
拓展应用:如图④,在△ABC中,AB=AC,AB>BC.点D在边BC上,CD=2BD,点E、F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为15,则△ACF与△BDE的面积之和为 .(12分)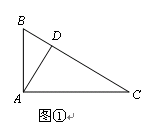
查看答案和解析>>
科目:初中数学 来源:2012-2013学年浙江湖州第八中学八年级10月月考数学试卷(解析版) 题型:解答题
问题情境:如图①,在直角三角形ABC中,∠BAC=90°,AD⊥BC于点D,可知:∠BAD=∠C(不需要证明);
特例探究:如图②,∠MAN=90°,射线AE在这个角的内部,点B、C在∠MAN的边AM、AN上,且AB=AC, CF⊥AE于点F,BD⊥AE于点D.证明:△ABD≌△CAF;
归纳证明:如图③,点BC在∠MAN的边AM、AN上,点EF在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC, ∠1=∠2=∠BAC.求证:△ABE≌△CAF;
拓展应用:如图④,在△ABC中,AB=AC,AB>BC.点D在边BC上,CD=2BD,点E、F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为15,则△ACF与△BDE的面积之和为 .(12分)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com