Question

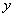某车间的甲、乙两名工人分别同时生产只同一型号的零件，他们生产的零件（只）与生产时间（分）的函数关系的图象如图所示。根据图象提供的信息解答下列问题：

（1）甲每分钟生产零件_______只；乙在提高生产速度之前已生产了零件_______只；

（2）若乙提高速度后，乙的生产速度是甲的倍，请分别求出甲、乙两人生产全过程中，生产的零件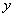（只）与生产时间（分）的函数关系式；

（3）当两人生产零件的只数相等时，求生产的时间；并求出此时甲工人还有多少只零件没有生产．

 

Answer 1

【答案】

（1）25，150；（2）y_甲=25x（0≤x≤20），y_乙=50x-350（10≤x≤17）；（3）150

【解析】

试题分析：（1）仔细分析函数图象的特征即可求得结果；

（2）仔细分析函数图象的特征根据待定系数法求解即可；

（3）先求得两个图象的交点坐标，即可求得结果.

（1）由图可得甲每分钟生产零件25只；乙在提高生产速度之前已生产了零件150只；

（2）由图可得甲：y_甲=25x（0≤x≤20），乙：y_乙=15x（0≤x≤10）

设y_乙=kx+b，把（10，150）（17，500）代入到

，解得

∴y_乙=50x-350（10≤x≤17）；

（3）令y_甲= y_乙得25x=50x-350，解得x=14   

此时y_甲= y_乙=350只，还有150只未生产.

考点：一次函数的应用

点评：函数的应用是初中数学的重点和难点，是中考常见题，一般难度不大，需熟练掌握.