
 如图,AB为⊙O的直径,直线CD切⊙O于点M,BE⊥CD于点E.
如图,AB为⊙O的直径,直线CD切⊙O于点M,BE⊥CD于点E.分析 (1)由切线的性质得出∠BME+∠OMB=90°,再由直径得出∠AMB=90°,利用同角的余角相等判断出结论;
(2)先在Rt△BEM中,用三角函数求出BM,再在Rt△ABM中,用三角函数和勾股定理计算即可.
解答 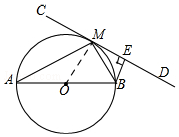 (1)如图,连接OM.
(1)如图,连接OM.
∵直线CD切⊙O于点M.
∴∠OMD=90°.
∴∠BME+∠OMB=90°.
∵AB为⊙O的直径.
∴∠AMB=90°.
∴∠AMO+∠OMB=90°.
∴∠BME=∠AMO.
∵OA=OM.
∴∠MAB=∠AMO.
∴∠BME=∠MAB;
(2)由(1)可得,∠BME=∠MAB.
∵sin∠BAM=$\frac{3}{5}$,
∴sin∠BME=$\frac{3}{5}$
在Rt△BEM中,BE=$\frac{18}{5}$.
∴sin∠BME=$\frac{BE}{BM}$=$\frac{3}{5}$.
∴BM=6,在Rt△ABM中,sin∠BAM=$\frac{3}{5}$.
∴sin∠BAM=$\frac{BM}{AB}$=$\frac{3}{5}$.
∴AB=$\frac{3}{5}$BM=10.
∴⊙O的半径=5
点评 本题主要考查了切线的性质,直径所对的圆周角是直径,相似三角形的性质和判定,三角函数,作出恰当的辅助线是解答此题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
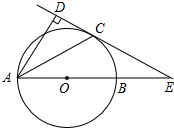 如图,以AB为直径的⊙O交∠BAD的角平分线于C,过C作CD⊥AD于D,交AB的延长线于E.
如图,以AB为直径的⊙O交∠BAD的角平分线于C,过C作CD⊥AD于D,交AB的延长线于E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
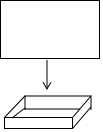 工人师傅用一块长为10dm,宽为6dm的矩形铁皮制作一个无盖的长方体容器,需要将四角各裁掉一个正方形.(厚度不计)
工人师傅用一块长为10dm,宽为6dm的矩形铁皮制作一个无盖的长方体容器,需要将四角各裁掉一个正方形.(厚度不计)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 销售价格x(元/千克) | 30 | 35 | 40 | 45 | 50 |
| 日销售量p(千克) | 600 | 450 | 300 | 150 | 0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
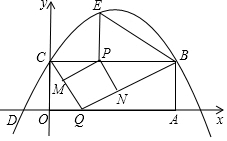 如图,矩形OABC的两边在坐标轴上,点A的坐标为(10,0),抛物线y=ax2+bx+4过点B,C两点,且与x轴的一个交点为D(-2,0),点P是线段CB上的动点,设CP=t(0<t<10).
如图,矩形OABC的两边在坐标轴上,点A的坐标为(10,0),抛物线y=ax2+bx+4过点B,C两点,且与x轴的一个交点为D(-2,0),点P是线段CB上的动点,设CP=t(0<t<10).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
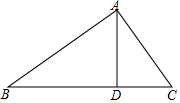 如图,△ABC中,∠BAC=90°,AD⊥BC,垂足为D.求作∠ABC的平分线,分别交AD,AC于P,Q两点;并证明AP=AQ.(要求:尺规作图,保留作图痕迹,不写作法)
如图,△ABC中,∠BAC=90°,AD⊥BC,垂足为D.求作∠ABC的平分线,分别交AD,AC于P,Q两点;并证明AP=AQ.(要求:尺规作图,保留作图痕迹,不写作法)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com