
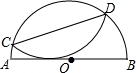
 半圆⊙O中,AB为直径,C、D为半圆上任意两点,将$\widehat{CD}$沿直线CD翻折使AB与$\widehat{CD}$相切,已知AB=8,求CD的最大值4$\sqrt{3}$.
半圆⊙O中,AB为直径,C、D为半圆上任意两点,将$\widehat{CD}$沿直线CD翻折使AB与$\widehat{CD}$相切,已知AB=8,求CD的最大值4$\sqrt{3}$. 分析 当CD∥AB时,有最大值,过O作CD的垂线交CD于点E,连接CO,利用折叠的性质,易得OE=$\frac{1}{2}$AO=$\frac{1}{2}$×4=2,利用勾股定理得CE,易得AD.
解答 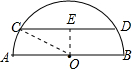 解:当CD∥AB时,有最大值,
解:当CD∥AB时,有最大值,
过O作CD的垂线交CD于点E,连接CO,
∴OE=$\frac{1}{2}$AO=$\frac{1}{2}$×4=2,CE=DE=$\frac{1}{2}$CD,
∵AB=8,
∴CE=$\sqrt{{CO}^{2}{-OE}^{2}}$=$\sqrt{{4}^{2}{-2}^{2}}$=2$\sqrt{3}$,
∴CD=4$\sqrt{3}$,
故答案为:4$\sqrt{3}$.
点评 本题主要考查了切线性质的运用“见切点,连半径,见垂直”,折叠的性质,分析出当CD∥AB时,有最大值,是解答此题的关键.


 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 套餐A | 套餐B | |
| 服务项目 | 国内通话+上网流量 | 国内通话+上网流量 |
| 每月基本服务费(座机费) | 59元 | 79元 |
| 免费通话时间 | 100分钟 | 200分钟 |
| 以后通话每分钟收费 | 0.25元 | 0.25元 |
| 免费上网流量 | 500MB | 700MB |
| 套外流量 | 不足100MB按0.4元/MB收费,达40元(即100MB)时,额外赠送400MB免费流量,当免费流量用完后,仍按0.4元/MB收费. | |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
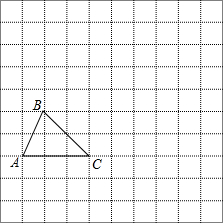 如图,在边长为1的小正方形组成的网络中,△ABC的顶点均在格点上,请按要求完成下列各题:
如图,在边长为1的小正方形组成的网络中,△ABC的顶点均在格点上,请按要求完成下列各题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
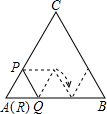 如图,正△ABC的边长为9cm,边长为3cm的正△RPQ的顶点R与点A重合,点P,Q分别在AC,AB上,将△RPQ沿着边AB,BC,CA连续翻转(如图所示),直至点P第一次回到原来的位置,则点P运动路径的长为6πcm.(结果保留π)
如图,正△ABC的边长为9cm,边长为3cm的正△RPQ的顶点R与点A重合,点P,Q分别在AC,AB上,将△RPQ沿着边AB,BC,CA连续翻转(如图所示),直至点P第一次回到原来的位置,则点P运动路径的长为6πcm.(结果保留π)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
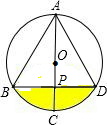 如图,已知在⊙O中,AB=4$\sqrt{3}$,AF=6,AC是直径,AC⊥BD于F,图中阴影部分的面积是( )
如图,已知在⊙O中,AB=4$\sqrt{3}$,AF=6,AC是直径,AC⊥BD于F,图中阴影部分的面积是( )| A. | $\frac{8}{3}$π-2$\sqrt{3}$ | B. | $\frac{16}{3}$π-2$\sqrt{3}$ | C. | $\frac{8}{3}$π-4$\sqrt{3}$ | D. | $\frac{16}{3}$π-4$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
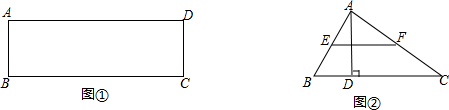
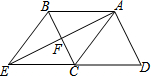 如图,四边形ABCD是平行四边形,点E为DC延长线上一点,联结AE,交BC边于点F,联结BE.
如图,四边形ABCD是平行四边形,点E为DC延长线上一点,联结AE,交BC边于点F,联结BE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
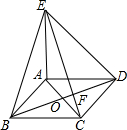 已知,已知?ABCD的对角线AC与BD相交于点O,△ABC和△ADE都是等腰直角三角形,且∠BAC=∠DAE=90°,连结BE,CE,且CE交BD于点F,现有四个结论:①BD=CE;②BD⊥CE;③∠ACE=∠ABE;④BF=EF,其中正确结论的个数为( )
已知,已知?ABCD的对角线AC与BD相交于点O,△ABC和△ADE都是等腰直角三角形,且∠BAC=∠DAE=90°,连结BE,CE,且CE交BD于点F,现有四个结论:①BD=CE;②BD⊥CE;③∠ACE=∠ABE;④BF=EF,其中正确结论的个数为( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com