
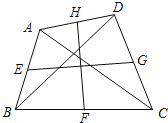
【题目】如图,在四边形ABCD中,AC=BD=6,E、F、G、H分别是AB、BC、CD、DA的中点,则EG2+FH2=______.
【答案】36。
【解析】
连接EF,FG,GH,EH,由E、F、G、H分别是AB、BC、CD、DA的中点,得到EH,EF,FG,GH分别是△ABD,△ABC,△BCD,△ACD的中位线,根据三角形中位线定理得到EH,FG等于BD的一半,EF,GH等于AC的一半,由AC=BD=6,得到EH=EF=GH=FG=3,根据四边都相等的四边形是菱形,得到EFGH为菱形,然后根据菱形的性质得到EG⊥HF,且EG=2OE,FH=2OH,在Rt△OEH中,根据勾股定理得到OE2+OH2=EH2=9,再根据等式的性质,在等式的两边同时乘以4,根据4=22,把等式进行变形,并把EG=2OE,FH=2OH代入变形后的等式中,即可求出EG2+FH2的值
如图,连接EF,FG,GH,EH,

∵E、H分别是AB、DA的中点,
∴EH是△ABD的中位线,
∴EH=![]() BD=3,
BD=3,
同理可得EF,FG,GH分别是△ABC,△BCD,△ACD的中位线,
∴EF=GH=![]() AC=3,FG=
AC=3,FG=![]() BD=3,
BD=3,
∴EH=EF=GH=FG=3,
∴四边形EFGH为菱形,
∴EG⊥HF,且垂足为O,
∴EG=2OE,FH=2OH,
在Rt△OEH中,根据勾股定理得:OE2+OH2=EH2=9,
等式两边同时乘以4得:4OE2+4OH2=9×4=36,
∴(2OE)2+(2OH)2=36,
即EG2+FH2=36.
故答案为:36.


科目:初中数学 来源: 题型:
【题目】某儿童游乐园门票价格规定如下表:
购票张数 | 1~50张 | 51~100张 | 100张以上 |
每张票的价格 | 13元 | 11元 | 9元 |
某校七年级(1)、(2)两个班共102人今年6.1儿童节去游该游乐园,其中(1)班人数较少,不足50人。经估算,如果两个班都以班为单位购票,则一共应付1218元。问:
(1)两个班各有多少学生?
(2)如果两班联合起来,作为一个团体购票,可以节省多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC 中,AB=AC,∠BAC=90°,D 是BC 上一点,EC⊥BC,EC=BD,DF=FE.

求证:(1)△ABD≌△ACE;
(2)AF⊥DE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从﹣4,﹣3,1,3,4这五个数中,随机抽取一个数,记为m,若m使得关于x,y的二元一次方程组 ![]() 有解,且使关于x的分式方程
有解,且使关于x的分式方程 ![]() ﹣1=
﹣1= ![]() 有正数解,那么这五个数中所有满足条件的m的值之和是( )
有正数解,那么这五个数中所有满足条件的m的值之和是( )
A.1
B.2
C.﹣1
D.﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】最近,“校园安全”受到全社会的广泛关注,重庆八中对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了如下两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
(1)扇形统计图中“基本了解”部分所对应扇形的圆心角为度;请补全条形统计图;
(2)若达到“了解”程度的人中有1名男生2名女生,达到“不了解”的程度的人中有1名男生和1名女生,若分别从达到“了解”程度和“不了解”的人中分别抽取1人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到1名男生和1名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD,等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,由下列条件可判定哪两条直线平行,并说明根据.

(1)∠1=∠2,________________________.
(2)∠A=∠3,________________________.
(3)∠ABC+∠C=180°,________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
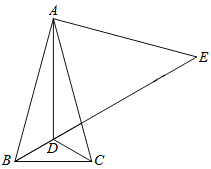
【题目】如图,在△ABC中,AB=AC,∠BAC=30°,点D是△ABC内一点,DB=DC,∠DCB=30°,点E是BD延长线上一点,AE=AB.
(1)求∠ADE的度数;
(2)求证:DE=AD+DC;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com