
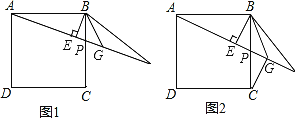
【题目】已知如图1,P为正方形ABCD的边BC上任意一点,BE⊥AP于点E,在AP的延长线上取点F,使EF=AE,连接BF,∠CBF的平分线交AF于点G.
(1)求证:BF=BC;
(2)求证:△BEG是等腰直角三角形;
(3)如图2,若正方形ABCD的边长为4,连接CG,当P点为BC的中点时,求CG的长.
【答案】(1)证明见解析;92)证明见解析;(3)![]()
【解析】(1)利用线段的垂直平分线的性质以及正方形的性质即可证明;
(2)想办法证明∠F=∠BAF=∠EBP,由∠EBG=∠EBP+∠PBG,∠EGB=∠F+∠GBF,即可解决问题;
(3)求出BG,只要证明△EBP≌△GCP,即可推出CG=BE,由此即可解决问题.
解:(1)证明:∵BE⊥AP,AE=EF,
∴BE垂直平分线段AF,
∴AB=BF,
在正方形ABCD中,AB=BC,
∴BF=BC;
(2)证明:∵四边形ABCD是正方形,
∴∠ABC=90°,
∴∠ABE+∠EBP=90°,
∵BE⊥AF,
∴∠ABE+∠BAP=90°,
∴∠BAP=∠EBP,
∵AB=BF∴∠BAP=∠BFP,
∴∠EBP=∠BFP,
∵∠CBF的平分线交AF于点G,
∴∠CBG=∠FBG,
∴∠EBP+∠CBG=∠BFP+∠FBG,
∴∠EBG=∠EGB,
∵BE⊥AF,
∴△BEG是等腰直角三角形.
(3)解:∵P是BC的中点,正方形的边长为4,
∴AB=4,BP=CP=2,
∵在Rt△ABP中,
∴AP=![]() ,
,
∵BE⊥AP,
∴S△ABP=![]() ,
,
解得:BE=![]() ,
,
∵AB=BC,AB=BF,
∴BC=BF,
由(1)可知∠CBG =∠FBG,
∴BG=BG,
∴△CBG≌△FBG,
∴∠BFP=∠BCG,
由(2)可知∠EBP=∠BFP,
∴∠EBP =∠BCG∵∠EPB =∠CPG,
∴△EBP≌△GCP,
∴CG=BE=![]() .
.
“点睛”本题考查正方形到现在、全等三角形的判定和性质、相等的垂直平分线的性质、等腰直角三角形的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考压轴题.


科目:初中数学 来源: 题型:
【题目】用配方法解方程x2+4x﹣1=0时,原方程应变形为( )
A. (x+2)2=5 B. (x+2)2=3 C. (x﹣2)2=3 D. (x﹣2)2=5
查看答案和解析>>
科目:初中数学 来源: 题型:
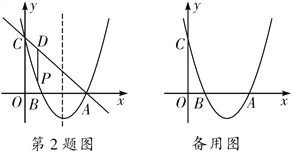
【题目】如图,抛物线y=x2+bx+c过点A(3,0),B(1,0),交y轴于点C,点P是该抛物线上一动点,点P从C点沿抛物线向A点运动(点P不与点A重合),过点P作PD∥y轴交直线AC于点D.
(1)求抛物线的解析式;
(2)求点P在运动的过程中线段PD长度的最大值;
(3)在抛物线对称轴上是否存在点M,使|MA-MC|最大?若存在,请求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名同学参加“古诗词大赛”活动,五次比赛成绩的平均分都是85分,如果甲比赛成绩的方差为S甲2=16.7,乙比赛成绩的方差为S乙2=28.3,那么成绩比较稳定的是_____(填甲或乙)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC在平面直角坐标系内(O为坐标原点),点A在x轴上,点C在y轴上,点B的坐标为(﹣4,﹣4![]() ),点E是BC的中点,现将矩形折叠,折痕为EF,点F为折痕与y轴的交点,EF交x轴于G且使∠CEF=60°.
),点E是BC的中点,现将矩形折叠,折痕为EF,点F为折痕与y轴的交点,EF交x轴于G且使∠CEF=60°.
(1)求证:△EFC≌△GFO;
(2)求点D的坐标;
(3)若点P(x,y)是线段EG上的一点,设△PAF的面积为s,求s与x的函数关系式并写出x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年某市约有108000名应届初中毕业生参加中考,按四舍五入保留两位有效数字,108000用科学计数法表示为( )
(A)0.10×106 (B)1.08×105 (C)0.11×106 (D)1.1×105
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com