
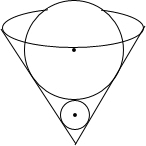
 如图,在一个轴截面为等边三角形的圆锥形容器内放置两个密度相同的金属球,两球均与容器壁紧贴,且大球恰好压在小球上,则大球质量是小球的27倍.
如图,在一个轴截面为等边三角形的圆锥形容器内放置两个密度相同的金属球,两球均与容器壁紧贴,且大球恰好压在小球上,则大球质量是小球的27倍. 分析 根据相切两圆的性质结合直角三角形的性质得出$\frac{R}{r}$=3,进而利用球的体积公式得出答案.
解答 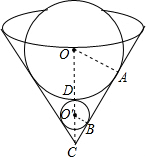 解:如图所示:由题意可得:∠OCA=30°,∠O′BC=∠OAC=90°,
解:如图所示:由题意可得:∠OCA=30°,∠O′BC=∠OAC=90°,
则设BO′=r,AO=R,
故CO=2R,CO′=2r,
则CD=3r=R,
故$\frac{R}{r}$=3,
∵大球的体积为:$\frac{4}{3}π{R}^{3}$=$\frac{4}{3}$π×(3r)3,小球的体积为:$\frac{4}{3}$πr3,
∴大球质量是小球的:$\frac{\frac{4}{3}π×27{r}^{3}}{\frac{4}{3}π×{r}^{3}}$=27.
故答案为:27倍.
点评 此题主要考查了相切两圆的性质以及球的体积公式等知识,得出两球的半径关系是解题关键.


科目:初中数学 来源: 题型:填空题
 如图,点A在双曲线y=$\frac{2}{x}$上,点B在双曲线y=$\frac{k}{x}$上,且AB∥x轴,点C,D在x轴上.若四边形ABCD为矩形,且它的面积为3,则k=5.
如图,点A在双曲线y=$\frac{2}{x}$上,点B在双曲线y=$\frac{k}{x}$上,且AB∥x轴,点C,D在x轴上.若四边形ABCD为矩形,且它的面积为3,则k=5.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
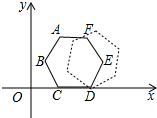 如图的平面直角坐标系中有一个正六边形ABCDEF,其中C、D的坐标分别为(1,0)和(2,0).若在无滑动的情况下,将这个六边形沿着x轴向右滚动,则在滚动过程中,这个六边形的顶点A、B、C、D、E、F中,会过点(47,2)的是点D.
如图的平面直角坐标系中有一个正六边形ABCDEF,其中C、D的坐标分别为(1,0)和(2,0).若在无滑动的情况下,将这个六边形沿着x轴向右滚动,则在滚动过程中,这个六边形的顶点A、B、C、D、E、F中,会过点(47,2)的是点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 推理说明题,按图填空,括号内注明理由.
推理说明题,按图填空,括号内注明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com