
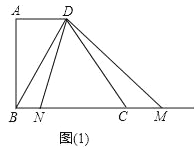
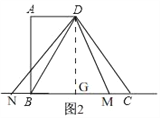
����Ŀ����֪��������ABCD�У�AD��BC����A=90�㣬AD=2��AB=4��BC=5��������BC��ȡһ��M������DM������MDN=��BDC����MDN����һ��DN��ֱ��BC�ڵ�N����N�ڵ�M����ࣩ��
��1����BM�ij�Ϊ10ʱ����֤��BD��DM��
��2����ͼ��1��������N���߶�BC��ʱ����BN=x��BM=y����y����x�ĺ�����ϵʽ����д�����Ķ�����
��3�������DMN�ǵ��������Σ���BN�ij���
���𰸡���1������������2��y=![]() ��0��x��4����3��BN=0��1��2
��0��x��4����3��BN=0��1��2![]() ��4��
��4��
�����������������
��1����ͼ1������D��DG��BC��G������֪���ı���ABGD�Ǿ��Σ���BG=AD=2��DG=AB=4����BC=5�ɵ�CG=3���ɹ��ɶ����ɵ�CD=5�����BM=10�ɵ�CM=BM-BC=5=BC=CD���ɴ˿ɵá�BDM��ֱ�������Σ��Ӷ��ɵ�BD��DM��
��2����ͼ1���ɣ�1����CD==5=BC�ɵá�BDC=��DBC��ϡ�MDN=��BDC���ɵõ���DBC=��MDN���ٽ�ϡ�BMD=��DMN�ɵá�MDN�ס�MBD���Ӷ��ɵ�DM2=BM��MN���DM2=DG2+MG2=16+��y��2��2��MN=BM��BN=y��x���ɵ�16+��y��2��2=y��y��x���������ɵ�y=![]() ����ϵ�N���߶�BC�Ͽɵ�x��ȡֵ��Χ�ǣ�
����ϵ�N���߶�BC�Ͽɵ�x��ȡֵ��Χ�ǣ�![]() ��
��
��3���֣���DN=DM��II��DM=MN��III��MN=DN������������֪������ǰ�����ý��۽��з������㼴��.
���������
��1����ͼ1������D��DG��BC��G��
���BGD=90�㣬
�ߡ�A=90�㣬����ABCD�У�AD��BC��
���ABC=90�㣬
���ı���ABGD�Ǿ��Σ�BG=AD=2��DG=AB=4��
��BC=5��
��CG=BC��BG=3��
��Rt��CDG�У����ݹ��ɶ����ã�CD=5��
��BM=10��
��CM=BM��BC=5=BC=CD��
���BDM��ֱ�������Σ�
��BD��DM��
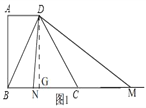
��2���ɣ�1��֪��CD=5=BC��
���BDC=��DBC��
�ߡ�MDN=��BDC��
���DBC=��MDN��
�ߡ�BMD=��DMN��
���MDN�ס�MBD��
��![]() ��
��
��DM2=BM��MN
��Rt��DMG�У����ݹ��ɶ����ã�DM2=DG2+MG2=16+��y��2��2��
��MN=BM��BN=y��x��
��16+��y��2��2=y��y��x����
��y=![]() ��
��
�֡ߵ�N���߶�BC�ϣ�
��0��x��4��
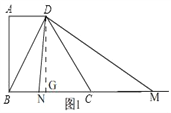
��3���ߡ�DMN�ǵ��������Σ�
��������DN=DMʱ����ͼ1��NG=MG��
��NG=2��x��MG=y��2��
��2��x=y��2��
��x+y=4����
�ɣ�2��֪��y=![]() ��
��
��y��4��x��=20��
�����٢ڣ����x=��![]() ��4���ᣩ��x=
��4���ᣩ��x=![]() ��4��
��4��
����BN=![]() -4��
-4��
������DM=MNʱ��
���MDN=��DNM��
�ߡ�CBD=��MDN��
���CBD=��DNM��
���N���B�غϣ�
��BN=0��
������MN=DNʱ��
���MDN=��DMN��
�ߡ�DBC=��MDN��
���DBC=��DMN��
��DM=BD��
��Rt��ABD�У����ݹ��ɶ����ã�BD2=AD2+AB2=20��
��DM2=16+��BM��2��2��
��20=16+��BM��2��2��
��BM=0����ȥ����BM=4��
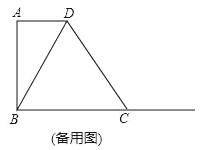
����ͼ2��
��M���߶�BC�ϣ�
ͬ��2���ķ����ã�16+��BM��2��2=BM��BM��BN������
��MN=BN+BM����
�����ۢܽ�ã�BN=1��
����BN=0��1��![]() ��4��
��4��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������ABCD�ı߳�Ϊ3��E��F�ֱ���AB��BC���ϵĵ㣬����EDF=45��������DAE�Ƶ�D��ʱ����ת90�����õ���DCM����AE=1����FM�ij�Ϊ ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
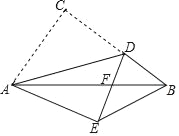
����Ŀ����ͼ����Rt��ABC�У���ACB=90�㣬AB=5��AC=3����D��BC��һ���㣬����AD������ACD��AD�۵�����C���ڵ�E��������DE��AB�ڵ�F������DEB��ֱ��������ʱ��DF�ij�Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ƽ��ֱ������ϵxOy�У���ͼ������֪������y=��x2+bx+c������A��2��2�����Գ�����ֱ��x=1������ΪB��
��1�������������ߵı���ʽ�͵�B�����ꣻ
��2����M�ڶԳ����ϣ���λ�ڶ����Ϸ���������������Ϊm������AM���ú�m�Ĵ���ʽ��ʾ��AMB������ֵ��
��3���������������ϻ�����ƽ�ƣ�ʹ���������ߵĶ���C��x���ϣ�ԭ��������һ��Pƽ�ƺ�Ķ�Ӧ��Ϊ��Q�����OP=OQ�����Q�����꣮
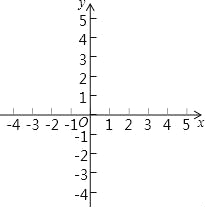
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
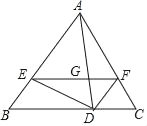
����Ŀ����ͼ�ڡ�ABC�У�AB=AC����D��E��F�ֱ��ڱ�BC��AB��AC�ϣ��ҡ�ADE=��B����ADF=��C���߶�EF���߶�AD�ڵ�G��
��1����֤��AE=AF��
��2����![]() ����֤���ı���EBDF��ƽ���ı��Σ�
����֤���ı���EBDF��ƽ���ı��Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
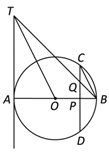
����Ŀ����ͼ��AB�ǡ�O��ֱ����AT�Ǿ�����A�����ߣ���CD��ֱAB��P�㣬QΪ�߶�CP���е㣬����BQ���ӳ�������AT��T�㣬����OT��
��1����֤��BC��OT��
��2������Oֱ��Ϊ10��CD��8����AT�ij���
��3���ӳ�TO��ֱ��CD��R������Oֱ��Ϊ10��CD��8����TR�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy������ֱ֪��AB��y![]() x+4��x���ڵ�A����y���ڵ�B��ֱ��CD��y
x+4��x���ڵ�A����y���ڵ�B��ֱ��CD��y![]() x��1��ֱ��AB�ཻ�ڵ�M����x���ڵ�C����y���ڵ�D��
x��1��ֱ��AB�ཻ�ڵ�M����x���ڵ�C����y���ڵ�D��
��1��ֱ��д����B�͵�D��������
��2������P������MD�ϵ�һ�����������P�ĺ�������x����PBM�������S����S��x֮��ĺ�����ϵ��
��3����S��20ʱ��ƽ��ֱ������ϵ���Ƿ���ڵ�E��ʹ�Ե�B��E��P��MΪ������ı�����ƽ���ı��Σ�����������ֱ��д�����з��������ĵ�E������������������˵��������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijũ����ֲһ�־����������ˮ��y����3������ֲʱ��x���죩֮��ĺ�����ϵʽͼ
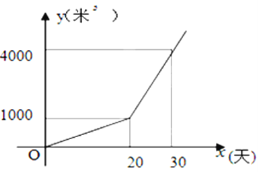
��1����20�������ˮ��Ϊ������3��
��2����x��20ʱ����y��x֮��ĺ�����ϵʽ��
��3����ֲʱ��Ϊ������ʱ������ˮ���ﵽ7000��3��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com