
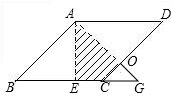
 如图,在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,将△ABE沿AE所在直线翻折后得△AGE,那么△AGE与四边形AECD重叠部分的面积是多少?
如图,在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,将△ABE沿AE所在直线翻折后得△AGE,那么△AGE与四边形AECD重叠部分的面积是多少? 分析 根据翻折得:△AEG≌△ABE,得AG=AB=2,且△ABE和△AGE是等腰直角三角形,再得△COG是等腰直角三角形,设OC=OG=x,则AO=2-x,CG=$\sqrt{2}$x,证明△ODA∽△OCG,得比例式求出x的值,分别求△AEG和△OCG的面积,并求其重叠部分的面积.
解答 解:∵在边长为2的菱形ABCD中,
∴AB=2,
∵∠B=45°,AE为BC边上的高,
∴AE=$\sqrt{2}$,
由折叠得:△AEG为等腰直角三角形,AG=AB=2,
∴∠AGE=45°,
∵四边形ABCD为菱形,
∴∠D=∠B=45°,
∵AD∥BC,
∴∠DCG=∠D=45°,
∴∠COG=90°,
∴△COG是等腰直角三角形,
∴${{S}_{△{AEG}}}=\frac{1}{2}{AE}•{EG}={1}$,
设OC=OG=x,则AO=2-x,CG=$\sqrt{2}$x,
∵AD∥CG,
∴△ODA∽△OCG,
得$\frac{AD}{CG}=\frac{AO}{GO}$,即$\frac{2}{{\sqrt{2}{x}}}=\frac{{{2}-{x}}}{x}$,
解得${x}={2}-\sqrt{2}$,
∴${{S}_{△{COG}}}=\frac{1}{2}{{x}^{2}}=\frac{1}{2}{({{2}-\sqrt{2}})^{2}}{=3}-{2}\sqrt{2}$,
∴重叠部分的面积为${{S}_{△{AEG}}}-{{S}_{△{COG}}}={1}-({{3}-{2}\sqrt{2}})={2}\sqrt{2}-{2}$.
点评 本题考查了菱形的性质、三角形面积和翻折变换问题,知道菱形的四边相等、对角相等;明确翻折前后的两个图形全等,求阴影部分面积时,观察图形形状,可以直接求解,也可以间接利用面积和或差来求.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知在平面直角坐标系中,B、C的坐标为(-10,0)、(-10,5),P、Q两点分别是x轴、y轴上的动点,且满足PQ=OC,问P、Q点运动到何处时,△OBC才能和以P、Q、O为顶点的三角形全等.
如图,已知在平面直角坐标系中,B、C的坐标为(-10,0)、(-10,5),P、Q两点分别是x轴、y轴上的动点,且满足PQ=OC,问P、Q点运动到何处时,△OBC才能和以P、Q、O为顶点的三角形全等.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com