
【题目】如图,要证明平行四边形ABCD为正方形,那么我们需要在四边形ABCD是平行四边形的基础上,进一步证明( )

A.AB=AD且AC⊥BDB.AB=AD且AC=BDC.∠A=∠B且AC=BDD.AC和BD互相垂直平分
 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
【题目】定义:若两个函数y1和y2的自变量x的取值范围相同,我们不妨把y1和y2的比值y称为x的比函数,且比函数的自变量x的取值范围不发生改变.例如:y1=x2+2x(x>0),y2=x(x>0),则x的比函数为y=![]() =x+2(x>0).
=x+2(x>0).
(1)已知y1=x2﹣4(2≤x≤3),y2=x+2(2≤x≤3),写出x的比函数y的解析式,并求出y的取值范围;
(2)已知y1=x+2(x>1),y2=x﹣2(x>1),求x的比函数y的图象上的整数点(横坐标和纵坐标都为整数的点)的坐标;
(3)已知y1=x2﹣x+1,y2=x2+x+1,若x的比函数y的图象与抛物线y3=x2+2x+k(k为常数)存在交点,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax(x﹣3)+c(a<0,0≤x≤3),反比例函数y=![]() (x>0,k>0)图象如图1所示,反比例函数y=
(x>0,k>0)图象如图1所示,反比例函数y=![]() (x>0,k>0)的图象经过点P(m,n),PM⊥x轴,垂足为M,PN⊥y轴,垂足为N;且OMON=12.
(x>0,k>0)的图象经过点P(m,n),PM⊥x轴,垂足为M,PN⊥y轴,垂足为N;且OMON=12.
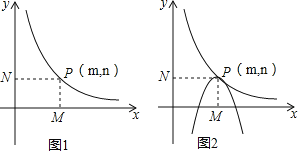
(1)求k的值;
(2)当c=0时,计算抛物线与x轴的两个交点之间的距离.
(3)确定二次函数y=ax(x﹣3)+c(a<0,0≤x≤3)对称轴.
(4)如图2,当a=﹣1时,抛物线y=ax(x﹣3)+c(a<0;0≤x≤3)有一时刻恰好经过P点,且此时抛物线与双曲线y=![]() (x>0,k>0)有且只有一个公共点P(如图2所示),我们不妨把此时刻的c记作c1,请直接写出抛物线y=ax(x﹣3)+c(a<0,0≤x≤3)的图象与双曲线y=
(x>0,k>0)有且只有一个公共点P(如图2所示),我们不妨把此时刻的c记作c1,请直接写出抛物线y=ax(x﹣3)+c(a<0,0≤x≤3)的图象与双曲线y=![]() (x>0,k>0)的图象有一个公共点时c的取值范围.(温馨提示:c1作为已知数,可直接应用哦!)
(x>0,k>0)的图象有一个公共点时c的取值范围.(温馨提示:c1作为已知数,可直接应用哦!)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有两个全等的含30°角的直角三角板重叠在一起,如图,将△A′B′C′绕AC的中点M转动,斜边A′B′刚好过△ABC的直角顶点C,且与△ABC的斜边AB交于点N,连接AA′、C′C、AC′.若AC的长为2,有以下五个结论:①AA′=1;②C′C⊥A′B′;③点N是边AB的中点;④四边形AA′CC′为矩形;⑤A′N=B′C=![]() ,其中正确的有( )
,其中正确的有( )
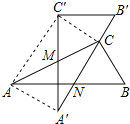
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣(2k+1)x+4k﹣3=0,
(1)求证:无论k取什么实数值,该方程总有两个不相等的实数根?
(2)当Rt△ABC的斜边a=![]() ,且两条直角边的长b和c恰好是这个方程的两个根时,求k的值.
,且两条直角边的长b和c恰好是这个方程的两个根时,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园读诗词诵经典比赛”结束后,评委刘老师将此次所有参赛选手的比赛成绩(得分均为整数)进行整理,并分别绘制成扇形统计图和频数直方图,部分信息如下图:

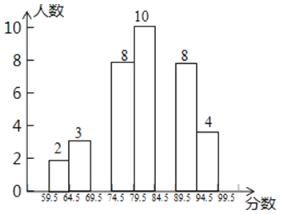
扇形统计图 频数直方图
(1)参加本次比赛的选手共有________人,参赛选手比赛成绩的中位数在__________分数段;补全频数直方图.
(2)若此次比赛的前五名成绩中有![]() 名男生和
名男生和![]() 名女生,如果从他们中任选
名女生,如果从他们中任选![]() 人作为获奖代表发言,请利用表格或画树状图求恰好选中
人作为获奖代表发言,请利用表格或画树状图求恰好选中![]() 男
男![]() 女的概率.
女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数![]() 的图象与正比例函数
的图象与正比例函数![]() 的图象交于点
的图象交于点![]() ,且
,且![]() 点的横坐标为2.
点的横坐标为2.
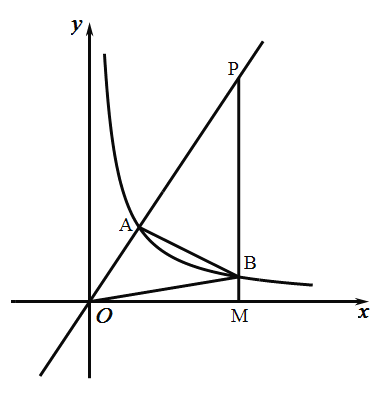
(1)求反比例函数的表达;
(2)若射线![]() 上有点
上有点![]() ,
,![]() ,过点
,过点![]() 作
作![]() 与
与![]() 轴垂直,垂足为点
轴垂直,垂足为点![]() ,交反比例函数图象于点
,交反比例函数图象于点![]() ,连接
,连接![]() ,
,![]() ,请求出
,请求出![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com