
【题目】在△ABC中,AB=AC=![]() , BC=2,以AB
, BC=2,以AB![]() 为直径的⊙O分别交AC、BC于点D、E。
为直径的⊙O分别交AC、BC于点D、E。
(1)求证:E是BC的中点;
(2)连结DE,求证:△CDE∽△CBA;
(3)求△CDE的面积.
【答案】
(1)证明:连接AE,
∵AB为⊙O的直径,
∴∠AED=90°,
即AE⊥BC,
又∵AB=AC,
∴E为BC中点.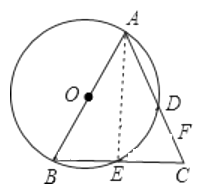
(2)证明:四边形是⊙O的内接四边形,
∴∠BED+∠BAD=180°,
又∵∠BED+∠DEC=180°,
∴∠BAD=∠DEC,
又∵∠BCA=∠DCE,
∴△CDE∽△CBA.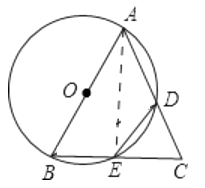
(3)解:由(1)知E为BC中点,
∵BC=2,
∴CE=BE=![]() BC=1,
BC=1,
由(2)知△CDE∽△CBA,
又∵AC=![]() ,
,
∴CE:CA=1:![]() ,
,
∴![]() =
=![]() ,
,
又由(1)知即AE⊥BC,
∴AE=![]() =2,
=2,
∴S△ABC=![]() .BC.AE=
.BC.AE=![]() ×2×2=2,
×2×2=2,
∴S△CDE=![]() S△ABC=
S△ABC=![]() ×2=
×2=![]() .
.
【解析】(1)连接AE,由圆周角定理得出∠AED=90°,又由等腰三角形的性质得出E为BC中点.
(2)由圆的内接四边形和邻补角定义得出∠BAD=∠DEC,又由∠BCA=∠DCE,根据相似三角形的判定:两个对应角相等的三角形相似即可得证.
(3)由(1)知E为BC中点,结合已知得出CE=BE=![]() BC=1,再结合勾股定理得出AE=
BC=1,再结合勾股定理得出AE=![]() =2,又由(2)知△CDE∽△CBA,根据相似三角形的性质得出
=2,又由(2)知△CDE∽△CBA,根据相似三角形的性质得出![]() =
=![]() ,由S△ABC=
,由S△ABC=![]() .BC.AE=
.BC.AE=![]() ×2×2=2,得出S△CDE=
×2×2=2,得出S△CDE=![]() S△ABC=
S△ABC=![]() ×2=
×2=![]() .
.
【考点精析】利用三角形的面积和等腰三角形的性质对题目进行判断即可得到答案,需要熟知三角形的面积=1/2×底×高;等腰三角形的两个底角相等(简称:等边对等角).


科目:初中数学 来源: 题型:
【题目】已知:方程组![]() 的解x为非正数,y为负数.
的解x为非正数,y为负数.
(1)求a的取值范围;
(2)化简|a-3|+|a+2|;
(3)在a的取值范围中,当a为何整数时,不等式2ax+x>2a+1的解为x<1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于点E,交AC于点F,过点O作OD⊥AC于点D,下列四个结论:①BE=EF-CF;②∠BOC=90°+![]() ∠A;③点O到△ABC各边的距离相等;④设OD=m,AE+AF=n,则S△AEF=
∠A;③点O到△ABC各边的距离相等;④设OD=m,AE+AF=n,则S△AEF=![]() mn,其中正确的结论是______.(填所有正确的序号)
mn,其中正确的结论是______.(填所有正确的序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形网格中,小格的顶点叫做格点.三个顶点都在网格上的三角形叫做格点三角形.小华已在左边的正方形网格中作出了格点△ABC.请你在右边的两个正方形网格中各画出一个不同的格点三角形,使得三个网格中的格点三角形都相似(不包括全等).
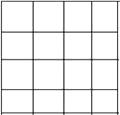

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列解题过程,然后解答后面两个问题.
解方程:|x-3|=2.
解:当x-3≥0时,原方程可化为x-3=2,解得x=5;
当x-3<0时,原方程可化为x-3=-2,解得x=1.
所以原方程的解是x=5或x=1.
(1)解方程:|3x-2|-4=0.
(2)解关于x的方程:|x-2|=b+1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道:有一内角为直角的三角形叫做直角三角形.类似地,我们定义:有一内角为45°的三角形叫做半直角三角形.如图,在平面直角坐标系中,O为原点,A(4,0),B(-4,0),D是y轴上的一个动点,∠ADC=90°(A、D、C按顺时针方向排列), BC与经过A,B,D三点的⊙M交于点E,DE平分∠ADC,连结AE,BD.显然△DCE,△DEF,△DAE是半直角三角形.
(1)求证:△ABC是半直角三角形;
(2)求证:∠DEC=∠DEA;
(3)若点D的坐标为(0,8),
①求AE的长;
②记BC与AD的交点为F,求ΔACF与ΔBCA的面积之比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题正确的是( )
A.方程x2-4x+2=0无实数根;
B.两条对角线互相垂直且相等的四边形是正方形
C.甲、乙、丙三人站成一排合影留念,则甲、乙二人相邻的概率是 ![]()
D.若 ![]() 是反比例函数,则k的值为2或-1。
是反比例函数,则k的值为2或-1。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数 ![]() ,自变量x与函数y的对应值如下表:
,自变量x与函数y的对应值如下表:
x | … | -5 | -4 | -3 | -2 | -1 | 0 | … |
y | … | 4 | 0 | -2 | -2 | 0 | 4 | … |
下列说法正确的是( )
A.抛物线的开口向下
B.当x>-3时,y随x的增大而增大
C.二次函数的最小值是-2
D.抛物线的对称轴x= ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】位于南岸区黄桷垭的文峰塔,有着“平安宝塔”之称.某校数学社团对其高度 AB进行了测量.如图,他们从塔底A的点B出发,沿水平方向行走了13米,到达点C,然后沿斜坡CD继续前进到达点D处,已知DC=BC.在点D处用测角仪测得塔顶A的仰角为42°(点A,B,C,D,E在同一平面内).其中测角仪及其支架DE高度约为0.5米,斜坡CD的坡度(或坡比)i=1:2.4,那么文峰塔的高度AB约为( )(sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)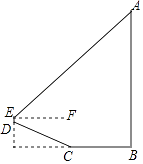
A.22.5 米
B.24.0 米
C.28.0 米
D.33.3 米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com