
| ���� | �� | 1 | 2 | 3 | 4 | 5 | 6 | �� |
| ��� | �� | $\frac{1}{2}$ | $\frac{2}{5}$ | $\frac{3}{10}$ | $\frac{4}{17}$ | $\frac{5}{26}$ | $\frac{6}{37}$ | �� |
���� �����������������ݱ����ɵ�������ݵķ��ӵ����������ݣ���ĸ�����������ݵ�ƽ����1�ĺͣ�
��1���������ݵó��𰸼��ɣ�
��2������ĸ��ʾ�����ɼ��ɣ�
��� �⣺��1������������10ʱ�������������$\frac{10}{1{0}^{2}+1}$=$\frac{10}{101}$��
��2������������nʱ�������������$\frac{n}{{n}^{2}+1}$��
�ʴ�Ϊ��$\frac{10}{101}$��$\frac{n}{{n}^{2}+1}$��
���� ���⿼�����ֵı仯���ɣ�������Ĺؼ��Ƿ�������������ݵķ��ӵ����������ݣ���ĸ�����������ݵ�ƽ����1�ĺͣ�


 ������ϰ�ο����뵥Ԫ���ϵ�д�
������ϰ�ο����뵥Ԫ���ϵ�д� �����Ծ���ĩ���100��ϵ�д�
�����Ծ���ĩ���100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ������������
�������������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ���߸ߵĽ��� | B�� | ���ǽ�ƽ���ߵĽ��� | ||
| C�� | �������ߵĽ��� | D�� | �����д��ߵĽ��� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
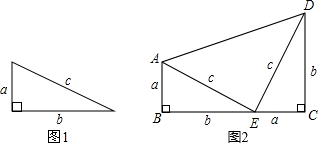
 ��ͼ����֪AD��BD��AC��BC��AC��BD���ڵ�F��EΪAB���е㣬
��ͼ����֪AD��BD��AC��BC��AC��BD���ڵ�F��EΪAB���е㣬�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ����⣺
����⣺�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
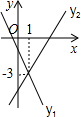 һ�κ���y1=k1x+b1��y2=k2x+b2��ͼ����ͼ��ʾ����x��1ʱ��y1��y2��
һ�κ���y1=k1x+b1��y2=k2x+b2��ͼ����ͼ��ʾ����x��1ʱ��y1��y2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
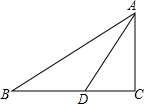 ��ͼ����֪��Rt��ABC�У���C=90�㣬D��BC����һ�㣬AD=$\sqrt{5}$����CAD=��ABC=������tan��=$\frac{1}{2}$����BD�ij�Ϊ��������
��ͼ����֪��Rt��ABC�У���C=90�㣬D��BC����һ�㣬AD=$\sqrt{5}$����CAD=��ABC=������tan��=$\frac{1}{2}$����BD�ij�Ϊ��������| A�� | 2 | B�� | 3 | C�� | 4 | D�� | 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
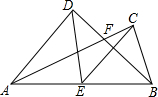
 ��ͼ���ڡ�ABC�У�ADƽ�֡�BAC��BC��D����AB�Ͻ�ȡAE=AC��
��ͼ���ڡ�ABC�У�ADƽ�֡�BAC��BC��D����AB�Ͻ�ȡAE=AC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
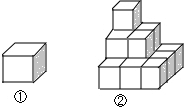
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com