

分析 (1)作DH∥BC交AE的延长线于H,先证明BD=HC,再证明HC=2CE即可解决.
(2)①结论AD+AB=2EC,作DH∥BC交CA的延长线于H,先证明BD=HC,再证明HC=2CE即可解决.
②结论AD+AB=2EC,作DH∥BC交CA的延长线于H,先证明BD=HC,再证明HC=2CE即可解决.
(3)利用图1、图2的结论计算即可,图3不合题意.
解答 (1)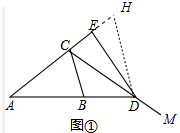 证明:如图1中,作DH∥BC交AE的延长线于H.
证明:如图1中,作DH∥BC交AE的延长线于H.
∵AC=AB,
∴∠ACB=∠ABC,
∵BC∥DH,
∴∠ACB=∠H,∠ABC=∠ADN,
∴∠H=∠ADH,
∴AD=AH,
∴BD=CH,
∵∠BCD=∠A,∠HCB=∠A+∠ABC,
∴∠HCB=∠ABC=∠H,
∴DC=DH,
∵DE⊥CH,
∴CE=EH,
∴HC=2EC,
∴AD-AB=BD=CH=2EC.
(2)①如图2中结论:AB+AD=2EC,理由如下: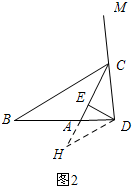 证明:作DH∥BC交CA的延长线于H.
证明:作DH∥BC交CA的延长线于H.
∵AC=AB,
∴∠ACB=∠ABC,
∵BC∥DH,
∴∠ACB=∠H,∠ABC=∠ADN,
∴∠H=∠ADH,
∴AD=AH,
∴BD=CH,
∵∠BCM+∠BCA+∠HCD=180°,∠BAC+∠B+∠BCA=180°,
∵∠BCM=∠BAC,
∴∠HCD=∠B=∠H,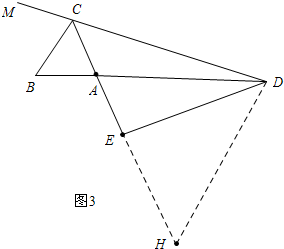
∴DC=DH,
∵DE⊥CH,
∴CE=EH,
∴HC=2EC,
∴AD-AB=BD=CH=2EC.
②如图3中,结论:AB+AD=2FC,理由如下:
作DH∥BC交CA的延长线于H.
∵AC=AB,
∴∠ACB=∠ABC,
∵BC∥DH,
∴∠ACB=∠H,∠ABC=∠ADN,
∴∠H=∠ADH,
∴AD=AH,
∴BD=CH,
∵∠BCM+∠BCA+∠HCD=180°,∠BAC+∠B+∠BCA=180°,
∵∠BCM=∠BAC,
∴∠HCD=∠B=∠H
∴DC=DH,
∵DE⊥CH,
∴CE=EH,
∴HC=2EC,
∴AD-AB=BD=CH=2EC.
(3)解:在图1中,∵AD-AB=2EC,AB=AC=3,EC=2,
∴AD-3=4
∴AD=7,
在图2中,∵AD+AB=2EC,AB=AC=3,CE=2,
∴AD+3=4,
∴AD=1,
在图3中,∵AC<CE不合题意.
故答案为7或1.
点评 本题考查等腰三角形性质、平行线的性质,通过作平行线构造等腰三角形是解决问题的关键.


科目:初中数学 来源:2016-2017学年江西省新余市八年级下学期第一次段考数学试卷(解析版) 题型:填空题
对于任意两个和为正数的实数a、b,定义运算※如下:a※b= 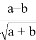 ,例如3※1=
,例如3※1=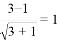 .那么8※12= ______ .
.那么8※12= ______ .
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江西省新余市八年级下学期第一次段考数学试卷(解析版) 题型:单选题
下列各式计算正确的是( )
A. 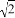 +
+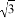 =
=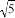 B. 4
B. 4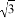 -3
-3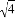 =1
=1
C. 2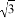 ×3
×3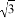 =6 D.
=6 D. 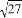 ÷
÷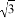 =3
=3
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,四边形ABCD中,∠BAD=90°,对角线AC与BD相交于点O,BO=DO,点E、F分别是AD、AC的中点.
如图,四边形ABCD中,∠BAD=90°,对角线AC与BD相交于点O,BO=DO,点E、F分别是AD、AC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com