
【题目】已知平行四边形ABCD,过点A作BC的垂线,垂足为点E,且满足AE=EC,过点C作AB的垂线,垂足为点F,交AE于点G,连接BG.

(1)如图1,若AC=![]() ,CD=4,求BC的长度;
,CD=4,求BC的长度;
(2)如图2取AC上一点Q,连接EQ,在△QEC内取一点,连接QH,EH,过点H作AC的垂线,垂足为点P,若QH=EH,∠QEH=45°.求证:AQ=2HP.
【答案】(1)3+![]() ;(2)见解析
;(2)见解析
【解析】
(1)利用勾股定理分别求出AE,BE即可解决问题.
(2)如图2中,如图2中,作EM⊥QE交QH的延长线于M,连接CM.证明△ABQ≌△CEM(SAS),推出AQ=CM,再利用三角形的中位线定理解决问题即可.
(1)解:如图1中,
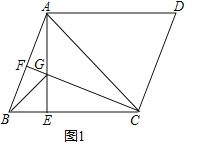
∵AE⊥BC于E,
∴∠AEC=90°,
∵AE=EC,AC=![]() ,
,
∴AE=EC=![]() ,
,
∵四边形ABCD是平行四边形,
∴AB=CD=4,
∵∠AEB=90°,
∴BE=![]() ,
,
∴BC=BE+EC=3+![]() .
.
(2)证明:如图2中,如图2中,作EM⊥QE交QH的延长线于M,连接CM.
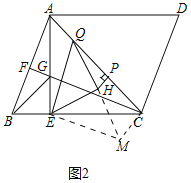
∵QH=EH,∠QEH=45°,
∴∠QEH=∠EQH=45°,
∴∠EHQ=90°,
∵EM⊥EQ,
∴∠MEQ=90°,
∴∠EMQ=∠EQM=45°,
∴EQ=EM,
∵EH⊥QM,
∴QH=HM,
∵∠AEC=∠QEM=90°,
∴∠AEQ=∠CEM,
∵EA=EC,EQ=EM,
∴△AEQ≌△CEM(SAS),
∴AQ=CM,∠EAQ=∠ECM=45°,
∵∠ACE=45°,
∴∠ACM=90°,
∵HP⊥QC,
∴∠HPQ=∠MCP,
∴HP∥CM,
∴QP=PC,
∵QH=HM,
∴CM=2PH,
∴AQ=2PH.


科目:初中数学 来源: 题型:
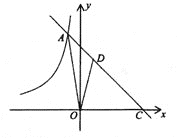
【题目】如图,在平面直角坐标系![]() 中,函数
中,函数![]() 的图象与函数
的图象与函数![]() 的图象相交于点A,并与
的图象相交于点A,并与![]() 轴交于点C,S△AOC=15.点D是线段AC上一点,CD:AC=2:3.
轴交于点C,S△AOC=15.点D是线段AC上一点,CD:AC=2:3.
(1)求![]() 的值;
的值;
(2)求点D的坐标;
(3)根据图象,直接写出当![]() 时不等式
时不等式![]() 的
的![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点M(n,﹣n )在第二象限,过点M的直线y=kx+b(0<k<1)分别交x轴、y轴于点A,B,过点M作MN⊥x轴于点N,则下列点在线段AN的是( )
A. ((k﹣1)n,0) B. ((k+![]() )n,0)) C. (
)n,0)) C. (![]() ,0) D. ((k+1)n,0)
,0) D. ((k+1)n,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
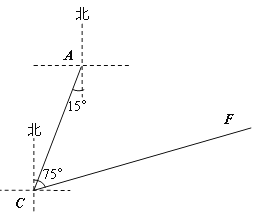
【题目】高考英语听力测试期间,需要杜绝考点周围的噪音。如图,点A是某市一高考考点,在位于A考点南偏西15°方向距离125米的![]() 点处有一消防队。在听力考试期间,消防队突然接到报警电话,告知在位于C点北偏东75°方向的F点处突发火灾,消防队必须立即赶往救火。已知消防车的警报声传播半径为100米,若消防车的警报声对听力测试造成影响,则消防车必须改道行驶。试问:消防车是否需要改道行驶?说明理由.(
点处有一消防队。在听力考试期间,消防队突然接到报警电话,告知在位于C点北偏东75°方向的F点处突发火灾,消防队必须立即赶往救火。已知消防车的警报声传播半径为100米,若消防车的警报声对听力测试造成影响,则消防车必须改道行驶。试问:消防车是否需要改道行驶?说明理由.(![]() 取1.732)
取1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司试销一种成本单价为50元/件的新产品,规定试销时销售单价不低于成本单价,又不高于80元/件,经试销调查,发现销售量y(件)与销售单价x(元/件)可近似看作一次函数y=kx+b的关系(如图所示)
(I)根据图象,求一次函数y=kx+b的解析式,并写出自变量x的取值范围;
(Ⅱ)该公司要想每天获得最大的利润,应把销售单价定为多少?最大利润值为多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点P(x0,m),Q(1,n)在二次函数y=(x+a)(x﹣a﹣1)(a≠0)的图象上,且m<n下列结论:①该二次函数与x轴交于点(﹣a,0)和(a+1,0);②该二次函数的对称轴是x=![]() ; ③该二次函数的最小值是(a+2)2; ④0<x0<1.其中正确的是_____.(填写序号)
; ③该二次函数的最小值是(a+2)2; ④0<x0<1.其中正确的是_____.(填写序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
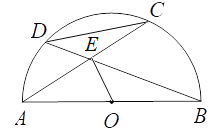
【题目】如图,以AB为直径的半圆O内有一条弦AC,点E是弦AC的中点,连接BE,并延长交半圆O于点D,若OB=2,OE=1,则∠CDE的度数是_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究:三角形的角平分线是初中几何中一条非常重要的线段,它除了具有平分角、角平分线上的点到角两边的距离相等这些性质外,还具有以下的性质:
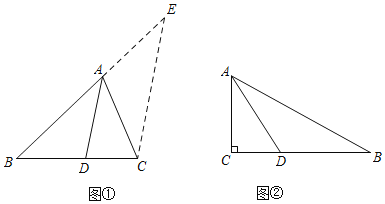
如图①,在△ABC中,AD平分∠BAC交BC于点D,则![]() =
=![]() .提示:过点C作CE∥AD交BA的延长线于点E.
.提示:过点C作CE∥AD交BA的延长线于点E.
请根据上面的提示,写出得到“![]() ”这一结论完整的证明过程.
”这一结论完整的证明过程.
结论应用:如图②,在Rt△ABC中,∠C=90°,AC=8,BC=15,AD平分∠BAC交BC于点D.请直接利用“问题探究”的结论,求线段CD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com