
如图,在边长为24cm的正方形纸片ABCD上,剪去图中阴影部分的四个全等的等腰直角三角形,再沿图中的虚线折起,折成一个长方体形状的包装盒(A.B.C.D四个顶点正好重合于上底面上一点).已知E、F在AB边上,是被剪去的一个等腰直角三角形斜边的两个端点,设AE=BF=x(cm).
(1)若折成的包装盒恰好是个正方体,试求这个包装盒的体积V;
(2)某广告商要求包装盒的表面(不含下底面)面积S最大,试问x应取何值?

 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
 8、如图,正方形ABCD边长为4cm,以正方形的一边BC为直径在正方形ABCD内作半圆,过A作半圆的切线,与半圆相切于F点,与DC相交于E点,则△ADE的面积( )
8、如图,正方形ABCD边长为4cm,以正方形的一边BC为直径在正方形ABCD内作半圆,过A作半圆的切线,与半圆相切于F点,与DC相交于E点,则△ADE的面积( )查看答案和解析>>
科目:初中数学 来源: 题型:
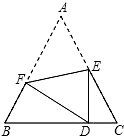 如图,已知边长为6的等边三角形ABC纸片,点E在AC边上,点F在AB边上,沿EF折F叠,使点A落在BC边上的点D的位置,且ED⊥BC,则CE的长为( )
如图,已知边长为6的等边三角形ABC纸片,点E在AC边上,点F在AB边上,沿EF折F叠,使点A落在BC边上的点D的位置,且ED⊥BC,则CE的长为( )A、24-12
| ||
B、12
| ||
C、12
| ||
D、18-12
|
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.21 | B.24 | C.33 | D.37 |
查看答案和解析>>
科目:初中数学 来源:第3章《圆》常考题集(15):3.2 点、直线与圆的位置关系,圆的切线(解析版) 题型:选择题
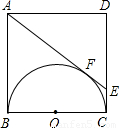
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com