
【题目】如图,四边形ABCD中,AB=AD=2,∠A=60°,BC=![]() ,CD=3.
,CD=3.
(1)求∠ADC的度数;
(2)求四边形ABCD的面积.

【答案】(1)150°; (2)![]()
【解析】试题分析:
(1)将△ABC绕点逆时针旋转60°,则有等边△ACC′,点D到等边△ACC′的距离符合勾股定理的逆定理,故将△ADC绕点A逆时针旋转60°,即可求解.
(2)将四边形ABCD分割为等边三角形和直角三角形,分别求出等边三角形和直角三角形的面积即可.
试题解析:
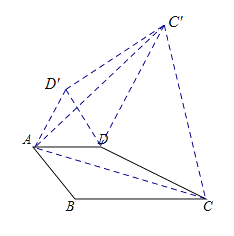
(1)如图,把△ABC绕点A逆时针旋转60°,构成三角形ACC′,把△ADC绕点A逆时针旋转60°,构成△AD′C.
由旋转的性质可知,△ACC′与△ADD′是等边三角形,且DC′=BC=![]() ,AD′=DD′=AD=2,D′C′=DC=3,∠AD′C=∠ADC.
,AD′=DD′=AD=2,D′C′=DC=3,∠AD′C=∠ADC.
因为DD′2=4,D′C′2=9,DC′2=13,所以DD′2+D′C′2=DC′2.
所以△DD′C′是直角三角形,所以∠DD′C′=90°,
因为∠AD′D=60°,所以∠AD′C=60°+90°=150°.
所以∠ADC=150°.
(2)由(1)知,S四边形ABCD=S四边形ADC′D′.
S四边形ADC′D′=S等边△ADD′+SRt△DD′C′=![]() =3+
=3+![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知AD是△ABC的角平分线,⊙O经过A、B、D三点,过点B作BE∥AD,交⊙O于点E,连接ED.
(1)求证:ED∥AC;
(2)连接AE,试证明:ABCD=AEAC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,七年级(1)班与七年级(2)班的学生分别在M、N两处参加植树劳动,现要设一个茶水供应点,使茶水供应点到两个班的距离相等(不写作法、要求保留作图痕迹).
(1)若茶水供应点P设在道路AB上,请你作出点P;
(2)若茶水供应点Q设在道路AB、AC的交叉区域内,并且使点Q到两条道路的距离相等,请你作出点Q.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中每个小方格都是边长为1个单位的正方形,若学校位置坐标为A(2,1),图书馆位置坐标为B(﹣1,﹣2),解答以下问题:
(1)在图中标出平面直角坐标系的原点,并建立直角坐标系;
(2)若体育馆位置坐标为C(1,﹣3),请在坐标系中标出体育馆的位置;
(3)顺次连接学校、图书馆、体育馆,得到△ABC,求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A=x﹣2y,B=﹣x﹣4y+1
(1)求3(A+B)﹣2(2A﹣B)的值;(结果用x、y表示)
(2)当 ![]() 与(y﹣1)2互为相反数时,求(1)中代数式的值.
与(y﹣1)2互为相反数时,求(1)中代数式的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一次同学聚会,他们的座位号是:小王的座位号与下列一组数中的负数的个数相等,小李的座位号与下列一组数中的正整数的个数相等,
6, ![]() ,0,200,
,0,200, ![]() ,5.22,0.01,+67,
,5.22,0.01,+67, ![]() ,10,300,24.
,10,300,24.
(1)若这次同学聚会的人数是小王的座位号的2倍与小李的座位号的4倍的和,请问这次聚会到了多少同学?
(2)试问小王、小李坐的各是第几号位置?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com