
 如图,等腰梯形ABCD的周长为6cm,∠B=45°,当腰长x(cm)为多少时,梯形面积y(cm)最大?并求出这个最大面积.
如图,等腰梯形ABCD的周长为6cm,∠B=45°,当腰长x(cm)为多少时,梯形面积y(cm)最大?并求出这个最大面积. 分析 作AM⊥BC于M,则∠AMB=90°,由等腰梯形的性质和已知条件得出AD+BC=(6-2x)cm,由三角函数得出AM=$\frac{\sqrt{2}}{2}$xcm,由梯形ABCD的面积=$\frac{1}{2}$(AD+BC)×AM,得出y=-$\frac{\sqrt{2}}{2}$(x-$\frac{3}{2}$)2+$\frac{9\sqrt{2}}{8}$,由-$\frac{\sqrt{2}}{2}$<0,得出y有最大值,即可得出结果.
解答 解:作AM⊥BC于M,如图所示: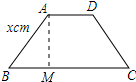
则∠AMB=90°,
∵四边形ABCD是等腰梯形,
∴AB=DC=xcm,
∴AD+BC=(6-2x)cm,
∵∠B=45°,
∴AM=AB•sin45°=$\frac{\sqrt{2}}{2}$xcm,
∵梯形ABCD的面积=$\frac{1}{2}$(AD+BC)×AM=$\frac{1}{2}$(6-2x)×$\frac{\sqrt{2}}{2}$x=-$\frac{\sqrt{2}}{2}$x2+$\frac{3\sqrt{2}}{2}$x=-$\frac{\sqrt{2}}{2}$(x-$\frac{3}{2}$)2+$\frac{9\sqrt{2}}{8}$(cm2),
∴y=-$\frac{\sqrt{2}}{2}$(x-$\frac{3}{2}$)2+$\frac{9\sqrt{2}}{8}$,
∵-$\frac{\sqrt{2}}{2}$<0,
∴y有最大值,
当x=$\frac{3}{2}$时,y最大,最大值=$\frac{9\sqrt{2}}{8}$;
即当腰长x(cm)为$\frac{3}{2}$cm时,梯形面积y(cm2)最大,这个最大面积为$\frac{9\sqrt{2}}{8}$cm2.
点评 本题考查了等腰梯形的性质、三角函数、二次函数的最值;熟练掌握等腰梯形的性质,根据梯形的面积公式得出y是x的二次函数是解决问题的关键.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 用4块大小相同的正方形硬纸片拼成一个大正方形(如图).小明在2m外投掷飞镖,假设飞镖击中一块小正方形是等可能的(击中小正方形边界线或没有击中大正方形,则重投1次).
用4块大小相同的正方形硬纸片拼成一个大正方形(如图).小明在2m外投掷飞镖,假设飞镖击中一块小正方形是等可能的(击中小正方形边界线或没有击中大正方形,则重投1次). 的概率.
的概率.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,点O是两个同心圆的圆心,大圆半径OA,OB交小圆于点C,D.下列结论中正确的个数有( )
如图,点O是两个同心圆的圆心,大圆半径OA,OB交小圆于点C,D.下列结论中正确的个数有( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com