
【题目】在平面直角坐标系xOy中,直线y=﹣x+2与x轴、y轴分别交于A、B两点,直线BC交x轴负半轴于点C,∠BCA=30°,如图①.
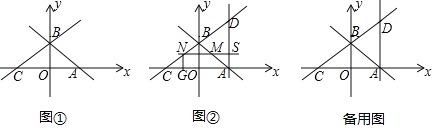
(1)求直线BC的解析式.
(2)在图①中,过点A作x轴的垂线交直线CB于点D,若动点M从点A出发,沿射线AB方向以每秒![]() 个单位长度的速度运动,同时,动点N从点C出发,沿射线CB方向以每秒2个单位长度的速度运动,直线MN与直线AD交于点S,如图②,设运动时间为t秒,当△DSN≌△BOC时,求t的值.
个单位长度的速度运动,同时,动点N从点C出发,沿射线CB方向以每秒2个单位长度的速度运动,直线MN与直线AD交于点S,如图②,设运动时间为t秒,当△DSN≌△BOC时,求t的值.
(3)若点M是直线AB在第二象限上的一点,点N、P分别在直线BC、直线AD上,是否存在以M、B、N、P为顶点的四边形是菱形.若存在,请直接写出点M的坐标;若不存在,请说明理由.
【答案】(1)y=![]() x+2;(2),t=
x+2;(2),t=![]() 秒或t=
秒或t=![]() +4秒时,△DSN≌△BOC;(3)M(
+4秒时,△DSN≌△BOC;(3)M(![]() +4)或M(
+4)或M(![]() )或M(
)或M(![]() ).
).
【解析】
(1)求出B,C的坐标,由待定系数法可求出答案;
(2)分别过点M,N作MQ⊥x轴,NP⊥x轴,垂足分别为点Q,P.分两种情况:(Ⅰ)当点M在线段AB上运动时,(Ⅱ)当点M在线段AB的延长线上运动时,由DS=BO=2,可得出t的方程,解得t的值即可得出答案;
(3)设点M(a,﹣a+2),N(b,![]() ),P(2,c),点B(0,2),分三种情况:(Ⅰ)当以BM,BP为邻边构成菱形时,(Ⅱ)当以BP为对角线,BM为边构成菱形时,(Ⅲ)当以BM为对角线,BP为边构成菱形时,由菱形的性质可得出方程组,解方程组即可得出答案.
),P(2,c),点B(0,2),分三种情况:(Ⅰ)当以BM,BP为邻边构成菱形时,(Ⅱ)当以BP为对角线,BM为边构成菱形时,(Ⅲ)当以BM为对角线,BP为边构成菱形时,由菱形的性质可得出方程组,解方程组即可得出答案.
解:(1)∵直线y=﹣x+2与x轴、y轴分别交于A、B两点,
∴x=0时,y=2,y=0时,x=2,
∴A(2,0),B(0,2),
∴OB=AO=2,
在Rt△COB中,∠BOC=90°,∠BCA=30°,
∴OC=2![]() ,
,
∴C(﹣2![]() , 0),
, 0),
设直线BC的解析式为y=kx+b,代入B,C两点的坐标得,
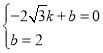 ,
,
∴k=![]() ,b=2,
,b=2,
∴直线BC的解析式为y=![]() x+2;
x+2;
(2)分别过点M,N作MQ⊥x轴,NP⊥x轴,垂足分别为点Q,P.
(Ⅰ)如图1,当点M在线段AB上运动时,
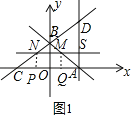
∵CN=2t,AM=![]() t,OB=OA=2,∠BOA=∠BOC=90°,
t,OB=OA=2,∠BOA=∠BOC=90°,
∴∠BAO=∠ABO=45°,
∵∠BCO=30°,
∴NP=MQ=t,
∵MQ⊥x轴,NP⊥x轴,
∴∠NPQ=∠MQA=90°,NP∥MQ,
∴四边形NPQM是矩形,
∴NS∥x轴,
∵AD⊥x轴,
∴AS∥MQ∥y轴,
∴四边形MQAS是矩形,
∴AS=MQ=NP=t,
∵NS∥x轴,AS∥MQ∥y轴,
∴∠DNS=∠BCO,∠DSN=∠DAO=∠BOC=90°,
∴当DS=BO=2时,
△DSN≌△BOC(AAS),
∵D(2, ![]() +2),
+2),
∴DS=![]() +2﹣t,
+2﹣t,
∴![]() +2﹣t=2,
+2﹣t=2,
∴t=![]() (秒);
(秒);
(Ⅱ)当点M在线段AB的延长线上运动时,如图2,
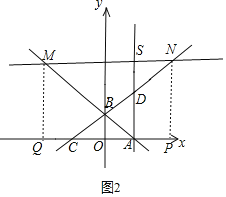
同理可得,当DS=BO=2时,△DSN≌△BOC(AAS),
∵DS=t﹣(![]() +2),
+2),
∴t﹣(![]() +2)=2,
+2)=2,
∴t=![]() +4(秒),
+4(秒),
综合以上可得,t=![]() 秒或t=
秒或t=![]() +4秒时,△DSN≌△BOC.
+4秒时,△DSN≌△BOC.
(3)存在以M、B、N、P为顶点的四边形是菱形:
M(﹣2![]() ﹣2,2
﹣2,2![]() +4)或M(﹣2
+4)或M(﹣2![]() ﹣4,2
﹣4,2![]() +6)或M(﹣2
+6)或M(﹣2![]() +2,2
+2,2![]() ).
).
∵M是直线AB在第二象限上的一点,点N,P分别在直线BC,直线AD上,
∴设点M(a,﹣a+2),N(b, ![]() b+2),P(2,c),点B(0,2),
b+2),P(2,c),点B(0,2),
(Ⅰ)当以BM,BP为邻边构成菱形时,如图3,

∵∠CBO=60°,∠OBA=∠OAB=∠PAF=45°,
∴∠DBA=∠MBN=∠PBN=75°,
∴∠MBE=45°,∠PBF=30°,
∴MB=![]() ME,PF=
ME,PF=![]() AP,PB=2PF=
AP,PB=2PF=![]() AP,
AP,
∵四边形BMNP是菱形,
∴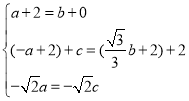 ,
,
解得,a=﹣2![]() ﹣2,
﹣2,
∴M(﹣2![]() ﹣2,2
﹣2,2![]() +4)(此时点N与点C重合),
+4)(此时点N与点C重合),
(Ⅱ)当以BP为对角线,BM为边构成菱形时,如图4,
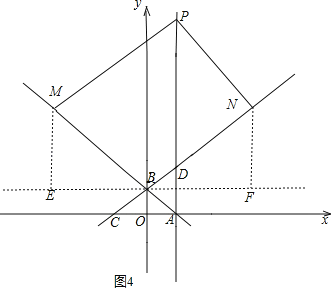
过点B作EF∥x轴,ME⊥EF,NF⊥EF,
同(Ⅰ)可知,∠MBE=45°,∠NBF=30°,
由四边形BMNP是菱形和BM=BN得:
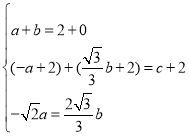 ,
,
解得:a=﹣2![]() ﹣4,
﹣4,
∴M(﹣2![]() ﹣4,2
﹣4,2![]() +6),
+6),
(Ⅲ)当以BM为对角线,BP为边构成菱形时,如图5,
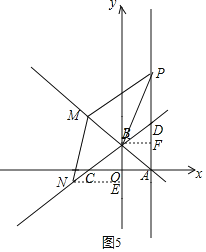
作NE⊥y轴,BF⊥AD,
∴∠BNE=30°,∠PBF=60°,
由四边形BMNP是菱形和BN=BP得,
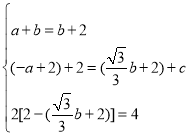 ,
,
解得:a=﹣2![]() +2,
+2,
∴M(﹣2![]() +2,2
+2,2![]() ).
).
综合上以得出,当以M、B、N、P为顶点的四边形是菱形时,点M的坐标为:
M(﹣2![]() ﹣2,2
﹣2,2![]() +4)或M(﹣2
+4)或M(﹣2![]() ﹣4,2
﹣4,2![]() +6)或M(﹣2
+6)或M(﹣2![]() +2,2
+2,2![]() ).
).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
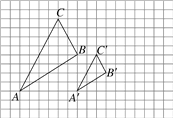
【题目】如图,△ABC与△A′B′C′是以点O为位似中心的位似图形,它们的顶点都在正方形网格的格点上.
(1)画出位似中心O;
(2)△ABC与△A′B′C′的相似比为__________,面积比为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
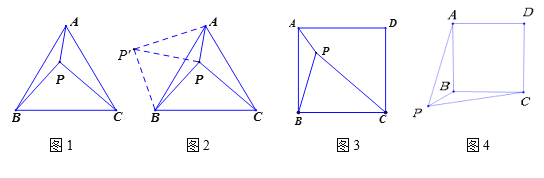
【题目】(问题提出)在数学“共生课堂”上,某合作小组提出了这样一个问题:如图1,在等边三角形ABC内有一点P,且PA=1,PB=2,PC=![]() .你能求出∠APB的度数吗?
.你能求出∠APB的度数吗?
(问题解决)(1)李清同学分析题目后,发现以PA、PB、PC的长为边的三角形是直角三角形,他找到了正确的思路:如图2,将△BPC绕点B逆时针旋转60°,得到△BP′A.连接PP′,易得△P′PB是等边三角形,△P′PA是直角三角形,则得∠BPP′=_________,∠APB=_________.
(问题类比)(2)同组的祁响同学突然想起曾经解决过的一个问题:如图3,点P是正方形ABCD内一点,PA=1,PB=2,PC=3.求∠APB的度数.请你写出解答过程.
(问题延伸)(3)夏老师留了一个思考题:如图4,若点P是正方形ABCD外一点,PA=![]() ,PB=1,PC=
,PB=1,PC=![]() .则∠APB的度数.请你写出解答过程.
.则∠APB的度数.请你写出解答过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着手机的普及,微信![]() 一种聊天软件
一种聊天软件![]() 的兴起,许多人抓住这种机会,做起了“微商”,很多农产品也改变了原来的销售模式,实行了网上销售,这不刚大学毕业的小明把自家的冬枣产品也放到了网上,他原计划每天卖100斤冬枣,但由于种种原因,实际每天的销售量与计划量相比有出入,下表是某周的销售情况
的兴起,许多人抓住这种机会,做起了“微商”,很多农产品也改变了原来的销售模式,实行了网上销售,这不刚大学毕业的小明把自家的冬枣产品也放到了网上,他原计划每天卖100斤冬枣,但由于种种原因,实际每天的销售量与计划量相比有出入,下表是某周的销售情况![]() 超额记为正,不足记为负
超额记为正,不足记为负![]() 单位:斤
单位:斤![]() ;
;
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
与计划量的差值 |
|
|
|
|
|
|
|
(1)根据记录的数据可知前三天共卖出 ______ 斤;
(2)根据记录的数据可知销售量最多的一天比销售量最少的一天多销售 ______ 斤;
(3)本周实际销售总量达到了计划数量没有?
(4)若冬季每斤按8元出售,每斤冬枣的运费平均3元,那么小明本周一共收入多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰直角三角形OAB中,∠OAB=90°,OA=AB,点D为OA中点,DC⊥OB,垂足为C,连接BD,点M为线段BD中点,连接AM、CM,如图①.

(1)求证:AM=CM;
(2)将图①中的△OCD绕点O逆时针旋转90°,连接BD,点M为线段BD中点,连接AM、CM、OM,如图②.
①求证:AM=CM,AM⊥CM;
②若AB=4,求△AOM的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】成都至西安的高速铁路(简称西成高铁)全线正式运营,至此,从成都至西安有两条铁路线可选择:一条是普通列车行驶线路(宝成线),全长825千米;另一条是高速列车行驶线路(西成高铁),全长660千米,高速列车在西成高铁线上行驶的平均速度是普通列车在宝成线上行驶的平均速度的3倍,乘坐普通列车从成都至西安比乘坐高速列车从成都至西安多用11小时,则高速列车在西成高铁上行驶的平均速度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示在平面直角坐标系中,方格纸中每个小方格都是边长为1个单位长度的正方形,已知点![]() ,
,![]() ,
,![]() .
.

(1)在所给的直角坐标系中画出三角形![]() ;
;
(2)把三角形![]() 向左平移3个单位,再向上平移2个单位得到三角形
向左平移3个单位,再向上平移2个单位得到三角形![]() ,画出三角形
,画出三角形![]() 并写出点
并写出点![]() 的坐标;
的坐标;
(3)求三角形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了测量被池塘隔开的A,B两点之间的距离,根据实际情况,作出如图所示的图形,其中AB⊥BE,EF⊥BE,AF交BE于点D,C在BD上.有四位同学分别测量出以下4组数据:①BC,∠ACB;②CD,∠ACB,∠ADB;③EF,DE,BD;④DE,DC,BC.能根据所测数据,求出A,B两点之间距离的有( )
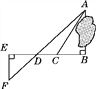
A. 1组 B. 2组 C. 3组 D. 4组
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自2019年11月20日零时起,大西高铁车站开始试点电子客票业务,旅客购票乘车更加便捷.大西高铁客运专线是国家《中长期铁路网规划》中的重要组成部分,它的建成将意味着今后山西人去西安旅行的路程与时间将大大缩短,但也有不少游客根据自己的喜好依然选择乘坐普通列车.已知高铁线路中从A地到某市的高铁行驶路程是400km,普通列车的行驶路程是高铁行驶路程的1.3倍,若高铁的平均速度(km/h)是普通列车平均速度(km/h)的2.5倍,且乘坐高铁所需时间比乘坐普通列车所需时间缩短3.6h,求普通列车和高铁的平均速度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com