
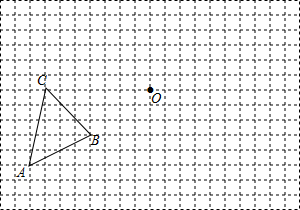
分析 (1)根据轴对称变换找出点A、B、C关于点O对称的点A1、B1、C1,顺次连接三点即可得出三角形A1B1C1;
(2)根据旋转变换找出点A、B、C以点O为中心按逆时针方向旋转90°后的对应点A2、B2、C2,顺次连接三点即可得出三角形A2B2C2.
解答 解:(1)分别找出点A、B、C关于点O对称的点A1、B1、C1,顺次连接三点即可得出三角形A1B1C1,如图1所示.

(2)连接AO、BO、CO,以点O为中心按逆时针方向旋转90°后,得到点A2、B2、C2,顺次连接三点即可得出三角形A2B2C2,如图2所示.
点评 本题考查了作图中的轴对称变换以及旋转变换,解题的关键是:(1)找到关于点O对称的点A1、B1、C1;(2)找到绕点O逆时针旋转90°的对应点A2、B2、C2.本题属于基础题,难度不大,解决该题型题目时,根据轴对称变换(或旋转变换)找出对称点(或对应点)是关键.


 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:解答题
 如图,△ABC是以BC为底边的等腰三角形,点A、C分别是一次函数$y=-\frac{3}{4}x+3$的图象与y轴、x轴的交点,点B在二次函数$y=\frac{1}{8}{x^2}+bx+c$的图象上,且该二次函数图象上存在一点D使四边形ABCD能构成平行四边形.
如图,△ABC是以BC为底边的等腰三角形,点A、C分别是一次函数$y=-\frac{3}{4}x+3$的图象与y轴、x轴的交点,点B在二次函数$y=\frac{1}{8}{x^2}+bx+c$的图象上,且该二次函数图象上存在一点D使四边形ABCD能构成平行四边形.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-3,3) | B. | (-3,6) | C. | (-1,5) | D. | (-1,6) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com