
分析 (1)令y=0,解关于x的一元二次方程即可得到顶点A的坐标;
(2)连接OB,确定出直线AB解析式,求出与y轴的交点D,进而求出$\frac{OD}{AD}$=$\frac{\sqrt{5}}{5}$,再求出$\frac{OB}{OA}$=$\frac{\sqrt{5}}{5}$,即$\frac{OD}{AD}=\frac{OB}{OA}$,得出△AOD∽△ABO,即∠ABO=∠AOD=90°,即可;
(3)利用待定系数法求出直线AB的解析式,再根据同底等高的三角形的面积相等,确定出线段AB的中点E和点C的直线解析式,与抛物线的交点即为所求的点P,然后联立抛物线与直线的解析式求解即可.
解答 解:(1)y=0,则(x-5)(x-a)=0,
解得x1=5,x2=a,
∴定点A的坐标为(5,0);
(2)如图,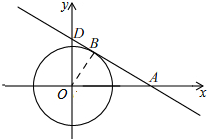
连接OB,由(1)A(5,0),
∴OA=5,
∵B(1,2),
∴直线AB解析式为y=-$\frac{1}{2}$x+$\frac{5}{2}$,
∴D(0,$\frac{5}{2}$),
∴OD=$\frac{5}{2}$,
在Rt△AOD中,AD=$\sqrt{O{A}^{2}+O{D}^{2}}$=$\frac{5\sqrt{5}}{2}$,
∴sin∠OAD=$\frac{OD}{AD}$=$\frac{\sqrt{5}}{5}$,
方法一,(判断∠ABO)
∵B(1,2),
∴OB=$\sqrt{5}$,
∴$\frac{OB}{OA}$=$\frac{\sqrt{5}}{5}$,
∴$\frac{OD}{AD}=\frac{OB}{OA}$
∵∠OAD=∠BAO,
∴△AOD∽△ABO,
∴∠ABO=∠AOD=90°,
方法二,(判断∠ABO)
∵B(1,2),
∴OB=$\sqrt{5}$,
∵A(5,0),
∴AB=2$\sqrt{5}$,OA=5,
∵AB2+OB2=25=AB2,
∴△ABO为直角三角形,
∴∠ABO=90°,
∵点B在⊙O上,
∴直线AB是⊙O的切线;
(3)存在点P($\frac{17}{3}$,$\frac{25}{9}$).
理由:∵抛物线y=(x-5)(x-a)过点B,
∴(1-5)(1-a)=2,
∴a=$\frac{3}{2}$,
∴y=(x-5)(x-a)=(x-5)(x-$\frac{3}{2}$);
∴C($\frac{3}{2}$,0)
如图,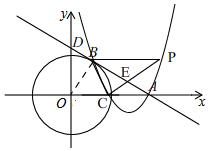 ,
,
∵△PAC、△PBC的面积相等,
∴S△PEB+S△BEC=S△PAE+S△AEC,
∴BE=AE,
∵B(1,2),A(5,0),
∴E(3,1),
∵C($\frac{3}{2}$,0),
∴直线CE的解析式为y=$\frac{2}{3}$x-1,
联立抛物线解析式y=(x-5)(x-$\frac{3}{2}$)和直线CE的解析式y=$\frac{2}{3}$x-1,
可得,$\left\{\begin{array}{l}{x=\frac{3}{2}}\\{y=0}\end{array}\right.$或$\left\{\begin{array}{l}{x=\frac{17}{3}}\\{y=\frac{25}{9}}\end{array}\right.$,
∵P在点A的右上方,
∴P($\frac{17}{3}$,$\frac{25}{9}$).
点评 本题是二次函数综合题型,主要考查了二次函数与x轴的交点问题,勾股定理的应用,直线与圆相切,相似三角形的判定与性质,同底等高的三角形的面积相等,(3)是本题的难点,考虑到点E是线段AB的中点求解是解题的关键.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案科目:初中数学 来源: 题型:填空题
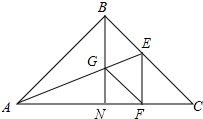 如图,在△ABC中,BA=BC,∠ABC=90°,BN平分∠ABC,AE平分∠BAC,AE交BN于G,EF⊥AC于F,连接GF.①△AEB≌△AEF;②∠EFG=∠AFG;③图中有3对全等三角形;④EF=GF;⑤S△AEF=2S△AGN.上述结论正确的序号有①②④⑤.
如图,在△ABC中,BA=BC,∠ABC=90°,BN平分∠ABC,AE平分∠BAC,AE交BN于G,EF⊥AC于F,连接GF.①△AEB≌△AEF;②∠EFG=∠AFG;③图中有3对全等三角形;④EF=GF;⑤S△AEF=2S△AGN.上述结论正确的序号有①②④⑤.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 有一个角是直角的四边形是矩形 | |
| B. | 对角线垂直的四边形是菱形 | |
| C. | 有一组邻边相等的四边形是菱形 | |
| D. | 对角线互相垂直平分且相等的四边形是正方形 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,PA和PB是⊙O的切线,点A和B是切点,AC是⊙O的直径,已知∠P=40°,则∠ACB的大小是( )
如图,PA和PB是⊙O的切线,点A和B是切点,AC是⊙O的直径,已知∠P=40°,则∠ACB的大小是( )| A. | 60° | B. | 65° | C. | 70° | D. | 75° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
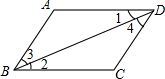 如图,下列推理是否正确,请写出你认为是正确推理的编号①②④.
如图,下列推理是否正确,请写出你认为是正确推理的编号①②④.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
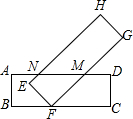 张萌的手中有长方形ABCD(AD∥BC)和长方形EFGH(EH∥FG)两张纸片,她将这两张纸片按如图所示的方式防置,是的FG,EH分别交AD于M,N两点,并测得∠MFC=30°,则∠ANH的度数为( )
张萌的手中有长方形ABCD(AD∥BC)和长方形EFGH(EH∥FG)两张纸片,她将这两张纸片按如图所示的方式防置,是的FG,EH分别交AD于M,N两点,并测得∠MFC=30°,则∠ANH的度数为( )| A. | 120° | B. | 130° | C. | 140° | D. | 150° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
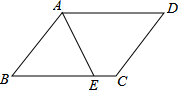 如图,平行四边形ABCD的周长为20cm,AE平分∠BAD,若CE=2cm,则AB的长度是( )
如图,平行四边形ABCD的周长为20cm,AE平分∠BAD,若CE=2cm,则AB的长度是( )| A. | 10cm | B. | 8cm | C. | 6cm | D. | 4cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
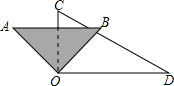 如图,将一副三角板的直角顶点重合在一起,将三角板AOB绕点O的旋转过程中,下列结论成立的是( )
如图,将一副三角板的直角顶点重合在一起,将三角板AOB绕点O的旋转过程中,下列结论成立的是( )| A. | ∠AOD>∠BOC | B. | ∠AOC≠∠BOD | C. | ∠AOD-∠BOC=45° | D. | ∠AOD+∠BOC=180° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
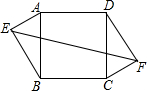 如图,在正方形ABCD中,AD=10,点E、F是正方形ABCD外的点,且AE=FC=6,BE=DF=8,则EF的长为( )
如图,在正方形ABCD中,AD=10,点E、F是正方形ABCD外的点,且AE=FC=6,BE=DF=8,则EF的长为( )| A. | 14 | B. | 16 | C. | $14\sqrt{2}$ | D. | $14\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com