
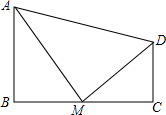
 如图,四边形ABCD中,∠B=90°,AB∥CD,M为BC边上的一点,且AM平分∠BAD,DM平分∠ADC.求证:
如图,四边形ABCD中,∠B=90°,AB∥CD,M为BC边上的一点,且AM平分∠BAD,DM平分∠ADC.求证:分析 (1)根据平行线的性质得到∠BAD+∠ADC=180°,根据角平分线的定义得到∠MAD+∠ADM=90°,根据垂直的定义得到答案;
(2)作NM⊥AD,根据角平分线的性质得到BM=MN,MN=CM,等量代换得到答案.
解答 解:(1)∵AB∥CD,
∴∠BAD+∠ADC=180°,
∵AM平分∠BAD,DM平分∠ADC,
∴2∠MAD+2∠ADM=180°,
∴∠MAD+∠ADM=90°,
∴∠AMD=90°,
即AM⊥DM;
(2)作NM⊥AD交AD于N,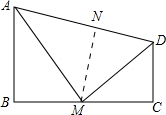
∵∠B=90°,AB∥CD,
∴BM⊥AB,CM⊥CD,
∵AM平分∠BAD,DM平分∠ADC,
∴BM=MN,MN=CM,
∴BM=CM,
即M为BC的中点.
点评 本题考查的是角平分线的性质,掌握平行线的性质和角的平分线上的点到角的两边的距离相等是解题的关键.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:选择题
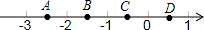 如图数轴上有A、B、C、D四点,根据图中各点的位置,判断那一点所表示的数与$\frac{\sqrt{2}}{2}$最接近的是( )
如图数轴上有A、B、C、D四点,根据图中各点的位置,判断那一点所表示的数与$\frac{\sqrt{2}}{2}$最接近的是( )| A. | A | B. | B | C. | C | D. | D |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 方程 | 一般形式 | 二次项系数 | 一次项系数 | 常数项 |
| (1)x2-x=2 | x2-x-2=0 | 1 | -1 | -2 |
| (2)4x+1=x2 | x2-4x-1=0 | 1 | -4 | -1 |
| (3)x(x+3)=-2 | x2+3x+2=0 | 1 | 3 | 2 |
| (4)(2x+1)(3x-2)=3 | 6x2-x-5=0 | 6 | -1 | -5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
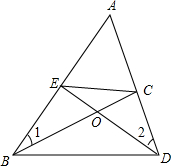 如图,△ABD中,点E、C分别在AB、AD上,BC与DE相交于点O,若∠1=∠2.求证:
如图,△ABD中,点E、C分别在AB、AD上,BC与DE相交于点O,若∠1=∠2.求证:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com