
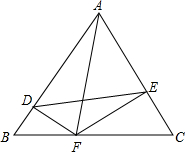
 △ABC为等边三角形,边长为a,DF⊥AB.EF⊥AC
△ABC为等边三角形,边长为a,DF⊥AB.EF⊥AC分析 (1)由等边三角形的性质得出∠B=∠C=60°,由已知得出∠BDF=∠CEF=90°,即可证出△BDF∽△CEF;
(2)作AM⊥BC于M,由等边三角形的性质得出AB=BC=4,BM=CM=$\frac{1}{2}$BC=2,由勾股定理求出AM,得出△ABC的面积;求出∠DFB=∠EFC=30°,由含30°角的直角三角形的性质得出BD=$\frac{1}{2}$BF=$\frac{1}{2}$m,CE=$\frac{1}{2}$CF=$\frac{1}{2}$(4-m),得出DF、EF的长度,求出△BDF和△CEF的面积,由四边形ADFE面积S=△ABC的面积-△BDF的面积-△CEF的面积,得出S与m之间的函数关系式为S=-$\frac{\sqrt{3}}{4}$m2+$\sqrt{3}$m+2$\sqrt{3}$;化成顶点式,得出当m=2时,S取最大值为3$\sqrt{3}$即可.
解答 (1)证明:∵△ABC为等边三角形,
∴∠B=∠C=60°,
∵DF⊥AB.EF⊥AC,
∴∠BDF=∠CEF=90°,
∴△BDF∽△CEF;
(2)解:作AM⊥BC于M,如图所示: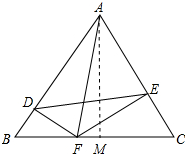
∵△ABC是等边三角形,
∴AB=BC=4,BM=CM=$\frac{1}{2}$BC=2,
∴AM=$\sqrt{A{B}^{2}-B{M}^{2}}$=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
∴△ABC的面积=$\frac{1}{2}$BC•AM=$\frac{1}{2}$×4×2$\sqrt{3}$=4$\sqrt{3}$,
∵BF=m,
∴CF=4-m,
∵∠BDF=∠CEF=90°,∠B=∠C=60°,
∴∠DFB=∠EFC=30°,
∴BD=$\frac{1}{2}$BF=$\frac{1}{2}$m,CE=$\frac{1}{2}$CF=$\frac{1}{2}$(4-m),
∴DF=$\sqrt{3}$BD=$\frac{\sqrt{3}}{2}$m,EF=$\sqrt{3}$CE=$\frac{\sqrt{3}}{2}$(4-m),
∴△BDF的面积=$\frac{1}{2}$BD•DF=$\frac{1}{2}$×$\frac{1}{2}$m×$\frac{\sqrt{3}}{2}$m=$\frac{\sqrt{3}}{8}$m2,
△CEF的面积=$\frac{1}{2}$CE•EF=$\frac{1}{2}$×$\frac{1}{2}$(4-m)×$\frac{\sqrt{3}}{2}$(4-m)=$\frac{\sqrt{3}}{8}$(4-m)2,
∴四边形ADFE面积S=△ABC的面积-△BDF的面积-△CEF的面积=4$\sqrt{3}$-$\frac{\sqrt{3}}{8}$m2-$\frac{\sqrt{3}}{8}$(4-m)2=-$\frac{\sqrt{3}}{4}$m2+$\sqrt{3}$m+2$\sqrt{3}$,
即S与m之间的函数关系式为S=-$\frac{\sqrt{3}}{4}$m2+$\sqrt{3}$m+2$\sqrt{3}$;
又∵S=-$\frac{\sqrt{3}}{4}$m2+$\sqrt{3}$m+2$\sqrt{3}$=-$\frac{\sqrt{3}}{4}$(m-2)2+3$\sqrt{3}$,-$\frac{\sqrt{3}}{4}$<0,
∴当m=2时,S取最大值为3$\sqrt{3}$.
点评 本题是相似形综合题目,考查了相似三角形的判定、等边三角形的性质、勾股定理、三角形面积的计算公式、含30°角的直角三角形的性质、二次函数的最值问题等知识;熟练掌握相似三角形的判定方法,求出S与m之间的函数关系式是解决问题(2)的关键.


 天天向上口算本系列答案
天天向上口算本系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,一只小猴顺着一根斜放的竹竿往上爬,眼睛一直盯着挂在上端的帽子,在小猴爬行的过程中,视线与水平方向所成角( )
如图,一只小猴顺着一根斜放的竹竿往上爬,眼睛一直盯着挂在上端的帽子,在小猴爬行的过程中,视线与水平方向所成角( )| A. | 逐渐变大 | B. | 逐渐变小 | C. | 不变 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | $\frac{1}{9}$ | C. | $\frac{1}{12}$ | D. | $\frac{1}{15}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,两个反比例函数y=$\frac{{k}_{1}}{x}$和y=$\frac{{k}_{2}}{x}$(其中k1>k2>0)在第一象限内的图象依次是Cl和C2,设点P在C1上,PC⊥x轴于点C,交C1于点A,PD上y轴于点D,交C2于点B,则四边形PAOB的面积为( )
如图,两个反比例函数y=$\frac{{k}_{1}}{x}$和y=$\frac{{k}_{2}}{x}$(其中k1>k2>0)在第一象限内的图象依次是Cl和C2,设点P在C1上,PC⊥x轴于点C,交C1于点A,PD上y轴于点D,交C2于点B,则四边形PAOB的面积为( )| A. | kl+k2 | B. | kl-k2 | C. | kl•k2 | D. | $\frac{{k}_{1}}{{k}_{2}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
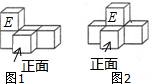 如图,图1是由5个完全相同的正方体堆成的几何体,现将标有E的正方体平移至如图2所示的位置,下列说法中正确的是( )
如图,图1是由5个完全相同的正方体堆成的几何体,现将标有E的正方体平移至如图2所示的位置,下列说法中正确的是( )| A. | 左、右两个几何体的主视图相同 | B. | 左、右两个几何体的左视图相同 | ||
| C. | 左、右两个几何体的俯视图不相同 | D. | 左、右两个几何体的三视图不相同 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
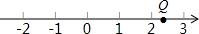 如图,数轴上的点Q所表示的数可能是( )
如图,数轴上的点Q所表示的数可能是( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | $\sqrt{10}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com