
 如图,点D、E三等分△ABC的BC边,求怔:AB+AC>AD+AE.
如图,点D、E三等分△ABC的BC边,求怔:AB+AC>AD+AE. 分析 取BC中点G,延长AG到H使得AG=GH,连接BH,DH,延长HD交AB于K,先证明:BH=AC,DH=AE,再根据BH+BK>KD+DH和AK+KD>AD,得到BH+BK+AK+KD>KD+DH+AD即BH+AB>DH+AD得到证明.
解答 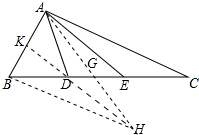 证明:取BC中点G,延长AG到H使得AG=GH,连接BH,DH,延长HD交AB于K.
证明:取BC中点G,延长AG到H使得AG=GH,连接BH,DH,延长HD交AB于K.
在△HBG和△GCA中,
$\left\{\begin{array}{l}{AG=GH}\\{∠AGC=∠BGH}\\{CG=BG}\end{array}\right.$,
∴△BGH≌△CGA,
∴AC=BH,同理可得DH=AE,
∵BH+BK>KH即BH+BK>KD+DH,
又∵AK+KD>AD,
∴BH+BK+AK+KD>KD+DH+AD,
∴BH+AB>DH+AD,
∵AC=BH,AE-DH,
∴AB+AC>AD+AE.
点评 本题考查三边关系定理、全等三角形的判定和性质,作三角形中线,把中线延长一倍是常用的辅助线.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:解答题
 “仅用刻度尺能画一个角的平分线吗?”小明想到了以下的方法:如图,在∠MON的边OM、ON上分别量取OA=OB,OC=OD;连结AD、BC交于点P.则射线OP就是∠MON的角平分线.
“仅用刻度尺能画一个角的平分线吗?”小明想到了以下的方法:如图,在∠MON的边OM、ON上分别量取OA=OB,OC=OD;连结AD、BC交于点P.则射线OP就是∠MON的角平分线.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
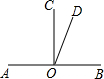 如图,直线AB过点O,OC、OD是直线AB同旁的两条射线,若∠BOD比∠COD的3倍还大20°,∠AOD比∠BOD的2倍小15°.求∠COD的度数.
如图,直线AB过点O,OC、OD是直线AB同旁的两条射线,若∠BOD比∠COD的3倍还大20°,∠AOD比∠BOD的2倍小15°.求∠COD的度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
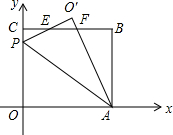 在平面直角坐标系中,O是坐标原点,矩OABC的位置如图所示,点A,C的坐标分别为(10,0),(0,8),点P是y轴上的一个动点,将△OAP沿AP翻折得到:△O′AP,直线BC与直线O′P交于点E,与直线O′A交于点F.
在平面直角坐标系中,O是坐标原点,矩OABC的位置如图所示,点A,C的坐标分别为(10,0),(0,8),点P是y轴上的一个动点,将△OAP沿AP翻折得到:△O′AP,直线BC与直线O′P交于点E,与直线O′A交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{a}{4}$ | B. | $\frac{1}{2}{x}^{2}$ | C. | $\frac{x}{π}$ | D. | $\frac{1}{a}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com