
 如图,AD为△ABC的高,BE为△ABC的角平分线,若∠EBA=34°,∠AEB=72°.
如图,AD为△ABC的高,BE为△ABC的角平分线,若∠EBA=34°,∠AEB=72°.分析 (1)根据角平分线定义求出∠CBE=∠EBA=34°,根据三角形外角性质求出∠C,即可求出答案;
(2)分为两种情况:当∠EFC=90°时,当∠FEC=90°时,求出即可.
解答 解:(1)∵BE为△ABC的角平分线,
∴∠CBE=∠EBA=34°,
∵∠AEB=∠CBE+∠C,
∴∠C=72°-34°=38°,
∵AD为△ABC的高,
∴∠ADC=90°,
∴∠CAD=90°-∠C=52°,
∠BAD=90°-∠ABD=90°-68°=22°;
(2)当∠EFC=90°时,∠BEF=90°-∠CBE=56°,
当∠FEC=90°时,∠BEF=180°-72°-90°=18°,
即∠BEF=56°或18°.
点评 本题考查了三角形内角和定理和三角形外角性质,能灵活运用三角形内角和定理求出角的度数是解此题的关键.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 宽与长的比是$\frac{\sqrt{5}-1}{2}$的矩形叫做黄金矩形.黄金矩形给我们以协调、匀称的美感.世界各国许多著名的建筑,为取得最佳的视觉效果,都采用了黄金矩形的设计.请用尺规作图的方法在方格纸中作出一个黄金矩形(自己确定边的长度)
宽与长的比是$\frac{\sqrt{5}-1}{2}$的矩形叫做黄金矩形.黄金矩形给我们以协调、匀称的美感.世界各国许多著名的建筑,为取得最佳的视觉效果,都采用了黄金矩形的设计.请用尺规作图的方法在方格纸中作出一个黄金矩形(自己确定边的长度)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
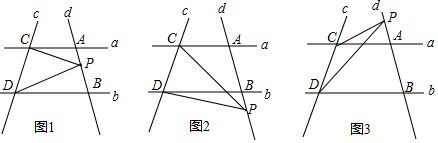
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
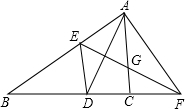 如图,在△ABC中,AD是∠BAC的平分线,AD的垂直平分线交AB于点E,交AC于点G,交BC的延长线于点F,连接AF、DE,下列结论:①△AEF≌△DEF②CF=AF-CD③DE∥AC④△AEG为等边三角形,其中正确结论有( )
如图,在△ABC中,AD是∠BAC的平分线,AD的垂直平分线交AB于点E,交AC于点G,交BC的延长线于点F,连接AF、DE,下列结论:①△AEF≌△DEF②CF=AF-CD③DE∥AC④△AEG为等边三角形,其中正确结论有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,把△ABC向上平移4个单位长度,再向右平移3个单位长度,得到△A′B′C′.
如图,把△ABC向上平移4个单位长度,再向右平移3个单位长度,得到△A′B′C′.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com