解:(1)设当0≤x≤100时y与x的函数关系式为y
1=k
1x,当x>100时y与x的函数关系式y
2=k
2x+b,由图象得:
10000=100k
1,
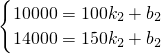
,
解得:k
1=100,
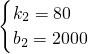
,
故y
1=100x,y
2=80x+2000;
(2)设方案1的付费总费用为W元,则购买300张票时付费为:W=10000+60×300=28000元,
方案2的付费为:y
2=80×300+2000=26000元,
∵28000>26000,
∴选择方案2.
(3)设采用方案1购买了x张,则用方案2购买了(700-x)张,由题意得:
10000+60x+80(700-x)+2000=58000,
解得:x=500,
故方案2买了700-500=200张.
或10000+60x+100(700-x)=58000.(700-x≤100),
解得:x=550
∴700-550=150>100(舍去)
答:甲、乙两个单位用方案1购买门票500张,用方案2购买门票200张.
分析:(1)设当0≤x≤100时y与x的函数关系式为y
1=k
1x,当x>100时y与x的函数关系式y
2=k
2x+b,根据图象由待定系数法可以直接求出结论;
(2)设方案1的付费总费用为W元,就可以根据购买的张数求出W的值,再与y
2比较就可以求出结论;
(3)设采用方案1购买了x张,则用方案2购买了(700-x)张,根据两种方案购买的总费用为58000元为等量关系建立方程,求其解救可以了.
点评:本题考查了待定系数法求一次函数的解析式的运用,方案设计的选择的运用及一元一次方程解实际问题的运用,再解答的过程中求出一次函数的解析式y
2=80x+2000是解答全题的关键.

 在购买某场篮球赛门票时,设购买门票张数为x(张),总费用为y(元).
在购买某场篮球赛门票时,设购买门票张数为x(张),总费用为y(元).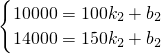 ,
,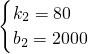 ,
,

 小学教材全测系列答案
小学教材全测系列答案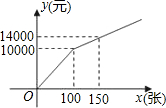 在购买某场篮球赛门票时,设购买门票张数为x(张),总费用为y(元).
在购买某场篮球赛门票时,设购买门票张数为x(张),总费用为y(元).