
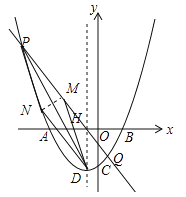
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�������![]() ��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C��0��
��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C��0��![]() ��������ΪD���Գ�����x�ύ�ڵ�H������H��ֱ��l����������P��Q���㣬��Q��y����Ҳ࣮
��������ΪD���Գ�����x�ύ�ڵ�H������H��ֱ��l����������P��Q���㣬��Q��y����Ҳ࣮
��1����a��ֵ����A��B�����ꣻ
��2����ֱ��l���ı���ABCD��Ϊ�����Ϊ3��7��������ʱ����ֱ��l�ĺ�������ʽ��
��3������Pλ�ڵڶ�����ʱ����PQ���е�ΪM����N���������ϣ�����DPΪ�Խ��ߵ��ı���DMPN�ܷ�Ϊ���Σ����ܣ������N�����ꣻ�����ܣ���˵�����ɣ�

���𰸡���1��![]() ��A����4��0����B��2��0������2��y��2x��2��
��A����4��0����B��2��0������2��y��2x��2��![]() ����3�����ڣ�N����
����3�����ڣ�N����![]() �� 1����
�� 1����
��������
�����������1���ѵ�C���������߽���ʽ�������a����y=0���з��̼��������A��B���꣮
��2��������ı���ABCD��������������Σ��ٵ�ֱ��l��AD�ཻ���M1ʱ������S��AHM1��![]() ��10��3�������M1���꼴�ɽ�����⣮�ڵ�ֱ��l��BC�ཻ���M2ʱ��ͬ���ɵõ�M2���꣮
��10��3�������M1���꼴�ɽ�����⣮�ڵ�ֱ��l��BC�ཻ���M2ʱ��ͬ���ɵõ�M2���꣮
��3����P��![]() ��
��![]() ����Q��
����Q��![]() ��
��![]() ���ҹ���H����1��0����ֱ��PQ�Ľ���ʽΪy=kx+b���õ�b=k�����÷����������M���꣬���ֱ��DN����ʽ�������÷����������N���꣬�г��������k�����ɽ�����⣮
���ҹ���H����1��0����ֱ��PQ�Ľ���ʽΪy=kx+b���õ�b=k�����÷����������M���꣬���ֱ��DN����ʽ�������÷����������N���꣬�г��������k�����ɽ�����⣮
�����������1������������y�ύ�ڵ�C��0��![]() ������a��3=
������a��3=![]() ����ã�
����ã�![]() ����
����![]()
��y=0ʱ����![]() ����
���� ![]() ��
��![]() ����A����4��0����B��2��0����
����A����4��0����B��2��0����
��2����A����4��0����B��2��0����C��0��![]() ����D����1����3��
����D����1����3��
��S�ı���ABCD=S��ADH+S����OCDH+S��BOC=![]() =10��
=10��
���������֪��ֱ��lֻ�����AD��BC�ཻ�����������������
�ٵ�ֱ��l��AD�ཻ���M1ʱ����S��AHM1��![]() ��10��3����
��10��3����![]() ��3������yM1����3����yM1����2����M1����2����2��������H����1��0����M1����2����2����ֱ��l�Ľ���ʽΪy=2x+2��
��3������yM1����3����yM1����2����M1����2����2��������H����1��0����M1����2����2����ֱ��l�Ľ���ʽΪy=2x+2��
�ڵ�ֱ��l��BC�ཻ���M2ʱ��ͬ���ɵõ�M2��![]() ����2��������H����1��0����M2��
����2��������H����1��0����M2��![]() ����2����ֱ��l�Ľ���ʽΪ
����2����ֱ��l�Ľ���ʽΪ![]() ��
��
����������ֱ��l�ĺ�������ʽΪy=2x+2��![]() ��
��
��3����P��![]() ��
��![]() ����Q��
����Q��![]() ��
��![]() ���ҹ���H����1��0����ֱ��PQ�Ľ���ʽΪy=kx+b���ੁk+b=0����b=k����y=kx+k��
���ҹ���H����1��0����ֱ��PQ�Ľ���ʽΪy=kx+b���ੁk+b=0����b=k����y=kx+k��
�� ����
����![]() ����
����![]() ��
��![]() ���ߵ�M���߶�PQ���е㣬�����е����깫ʽ�ĵ�M��
���ߵ�M���߶�PQ���е㣬�����е����깫ʽ�ĵ�M��![]() ��
��![]() ����
����
�������������N����ͼ��ֱ��DN��PQ����ֱ��DN�Ľ���ʽΪy=kx+k��3���� ����ã�
����ã�![]() ��
�� ![]() �� ��N��
�� ��N��![]() ��
��![]() ����
����
���ı���DMPN�����Σ���DN=DM����![]() �������ã�
�������ã�![]() ��
��![]() ����
���� ![]() ��0����
��0����![]() �����
�����![]() ����k��0����
����k��0����![]() ����P����
����P����![]() ��6����M����
��6����M����![]() ��2����N����
��2����N����![]() �� 1������PM=DN=
�� 1������PM=DN=![]() ����PM��DN�����ı���DMPN��ƽ���ı��Σ���DM=DN�����ı���DMPNΪ���Σ�����DPΪ�Խ��ߵ��ı���DMPN�ܳ�Ϊ���Σ���ʱ��N������Ϊ����
����PM��DN�����ı���DMPN��ƽ���ı��Σ���DM=DN�����ı���DMPNΪ���Σ�����DPΪ�Խ��ߵ��ı���DMPN�ܳ�Ϊ���Σ���ʱ��N������Ϊ����![]() ��1����
��1����


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijС��7��ͬѧ��������Լ����㻨Ǯ֧Ԯ�������������Ǿ�������ֱ��ǣ���λ��Ԫ����50��20��50��30��50��25��135���������ݵ���������λ���ֱ��ǣ� ����
A.50��20B.50��30C.50��50D.135��50
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2017������С���ٳ�ɳ�ص���������ԼΪ1900��1900���ÿ�ѧ��������ʾӦΪ��������
A. 19��104 B. 1.9��104 C. 1.9��107 D. 0.19��108
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���A=100�㣬BI��CI�ֱ�ƽ�֡�ABC����ACB�����BIC=________����BM��CM�ֱ�ƽ�֡�ABC����ACB�����ƽ���ߣ����M=__________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��
��һ�ּǷַ���80�����ϵģ���88�ּ���+8�֣�ij��ѧ����74�֣���Ӧ������ ����
A��+74�� B��+6�� C����6�� D����14��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�κ���y=��2��m��x��2�ĺ���ֵy��x���������С����m��ȡֵ��Χ�ǣ� ��
A.m��0
B.m��0
C.m��2
D.m��2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�BE��CF�ֱ���AC��AB�����ϵĸߣ���BE�Ͻ�ȡBD=AC����CF���ӳ����Ͻ�ȡCG=AB������AD��AG��
��1����֤��AD=AG
��2��AD��AG��λ�ù�ϵ���,��˵�����ɡ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڶ�������ɫ�ռ������Ĵ�����2020��1��12����ʽ�������������ݷ�Ϊ�����֣�������������������ɫ��������������λ��ί��������С�����������ֱַ�Ϊ��88��92��90��93��88�����������ݵ������� (����)
A.88B.90C.92D.93
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com