Question

（1）如图，在△ABC中，∠BAC=90°，AB=A C，点D在BC上，且BD=BA，点E在BC的延长线上，且CE=CA． 试求∠DAE的度数．

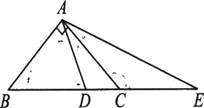
(2)如果把第(1)题中“AB=AC”的条件去掉，其余条件不变，那么∠DAE的度数会改变吗?

(3)如果把第(1)题中“∠BA C=90°”的条件改为“∠BAC>90°”。其余条件不变，那么∠DAE与∠BAC有怎样的大小关系? 并说明理由。

 

Answer 1

【答案】

（1）45度（2）不改变(3)

【解析】解：（1）∵AB＝AC，∠BAC＝90°

            ∴∠B＝∠ACB＝45°      …………………………………………1′

            ∵AB＝BD，AC＝CE，

            ∴∠BAD＝∠BDA，∠E＝∠CAE

            ∴……4′

           在△ABE中，∠BAE=180°-∠B-∠E=112.5°，

∴∠DAE=∠BAE-∠BAD=112.5°-67.5°=45度……………6′

（2）不改变．

设∠CAE=x，

∵CA=CE，

∴∠E=∠CAE=x，

∴∠ACB=∠CAE+∠E=2x，

在△ABC中，∠BAC=90°，

∴∠B=90°-∠ACB=90°-2x，

∵BD=BA，

∴∠BAD=∠BDA=（180°-∠B）=x+45°，

在△ABE中，∠BAE=180°-∠B-∠E，

=180°-（90°-2x）-x=90°+x，

∴∠DAE=∠BAE-∠BAD，

=（90°+x）-（x+45°）=45° ………………………………………7′

 （3）        ………………………………………8′

  设∠BAC＝α，因为

     所以

              ＝      ………………………………………10′

（1）要求∠DAE，必先求∠BAD和∠CAE，由∠BAC=90°，AB=AC，可求∠B=∠ACB=45°，又因为BD=BA，可求∠BAD=∠BDA=67.5°，再由CE=CA，可求∠CAE=∠E=22.5°，所以∠DAE=∠BAE-∠BAD=112.5°-67.5°=45度；

（2）先设∠CAE=x，由已知CA=CE可求∠ACB=∠CAE+∠E=2x，∠B=90°-2x，又因为BD=BA，所以∠BAD=∠BDA=x+45°，再根据三角形的内角和是180°，可求∠BAE=90°+x，即∠DAE=∠BAE-∠BAD=（90°+x）-（x+45°）=45度；

（3）可设∠BAC＝α，则 ＝