
 初三某班在庆祝申奥成功的活动中,制作某种喜庆用品需将一张半径为2的半圆形纸板沿它的一条弦折叠,使得弧与直径相切,如图所示,如果切点分直径为3:1两部分,则折痕长为( )
初三某班在庆祝申奥成功的活动中,制作某种喜庆用品需将一张半径为2的半圆形纸板沿它的一条弦折叠,使得弧与直径相切,如图所示,如果切点分直径为3:1两部分,则折痕长为( )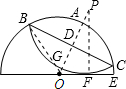
| 5 |
| 5 |
| 5 |
4-
| ||
| 2 |
| ||
| 2 |
| 5 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 11 |


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 次序 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 收入(元) | 7.80 | 8.40 | 6.50 | 7.80 | 5.30 | 9.70 | 8.20 | 9.20 |
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
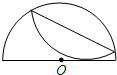 初三某班在庆祝申奥成功的活动中,制作某种喜庆用品需将一张半径为2的半圆形纸板沿它的一条弦折叠,使得弧与直径相切,如图所示,如果切点分直径为3:1两部分,则折痕长为
初三某班在庆祝申奥成功的活动中,制作某种喜庆用品需将一张半径为2的半圆形纸板沿它的一条弦折叠,使得弧与直径相切,如图所示,如果切点分直径为3:1两部分,则折痕长为



查看答案和解析>>
科目:初中数学 来源:2004年第2届“学用杯”全国数学知识应用竞赛九年级初赛试卷(解析版) 题型:选择题
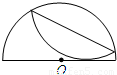
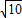

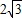
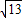
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com