
【题目】西安市某中学九年级组织了一次数学计算比赛(禁用计算器),每班选25名同学参加比赛,成绩分为A,B,C,D四个等级,其中A等级得分为100分,B等级得分为85分,C等级得分为75分,D等级得分为60分,数学教研组将九年级一班和二班的成绩整理并绘制成如下的统计图,请根据提供的信息解答下列问题.
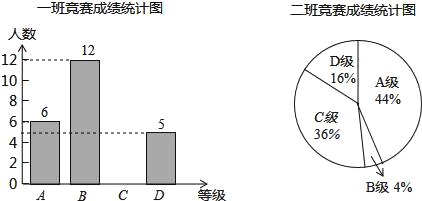
(1)把一班竞赛成绩统计图补充完整.
(2)填表:
平均数(分) | 中位数(分) | 众数(分) | |
一班 |
|
| 85 |
二班 | 84 | 75 |
|
(3)请从以下给出的两个方面对这次比赛成绩的结果进行①从平均数、众数方面来比较一班和二班的成绩;②从B级以上(包括B级)的人数方面来比较一班和二班的成绩.
【答案】(1)详见解析;(2)82.8、85、100;(3)①从平均数、众数方面来比较,二班成绩更好;②从B级以上(包括B级)的人数方面来比较,一班成绩更好.
【解析】
(1)根据题意和表格中的数据可以求得一班C等级的学生数,从而可以解答本题;
(2)根据表格中的数据可以求得一班的平均数和中位数,以及二班的众数;
(3)根据表格中的数据,可以从两方面比较一班和二班成绩的情况.
(1)一班C等级的学生有:25﹣6﹣12﹣5=2,
补全的条形统计图如右图所示;
(2)一班的平均数是:![]() =82.8,中位数是85,
=82.8,中位数是85,
二班的众数是100,
故答案为:82.8、85、100;
(3)①从平均数、众数方面来比较,二班成绩更好;
②从B级以上(包括B级)的人数方面来比较,一班成绩更好.


科目:初中数学 来源: 题型:
【题目】如图,将一张正方形纸片剪成四个小正方形,得到4个小正方形,称为第一次操作;然后,将其中的一个正方形再剪成四个小正方形,共得到7个小正方形,称为第二次操作;再将其中的一个正方形再剪成四个小正方形,共得到10个小正方形,称为第三次操作;…,根据以上操作,若要得到2011个小正方形,则需要操作的次数是( )
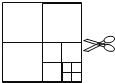
A. 669 B. 670 C. 671 D. 672
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.
与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.

(1)求该抛物线的解析式;
(2)当点P在直线BC上方时,请用含m的代数式表示PG的长度;
(3)在(2)的条件下,是否存在这样的点P,使得以P、B、G为顶点的三角形与△DEH相似?若存在,求出此时m的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是正△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①△BO′A可以由△BOC绕点B逆时针旋转60°得到;②点O与O′的距离为4;③∠AOB=150°;④S四边形AOBO′=6+3![]() .其中正确的结论有( )
.其中正确的结论有( )

A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,晚上小亮在广场上乘凉,图中线段AB表示站在广场上的小亮,线段PO表示直立在广场上的灯杆,点P表示照明灯.
请你再图中画出小亮在照明灯P照射下的影子BC;
如果灯杆高PO=12m,小亮的身高AB=1.6m,小亮与灯杆的距离BO=13m,请求出小亮影子的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
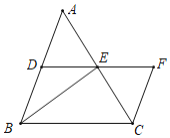
【题目】如图,在△ABC中,点D,E分别是边AB,AC的中点,过点C作CF∥AB交DE的延长线于点F,连接BE.
(1)求证:四边形BCFD是平行四边形.
(2)当AB=BC时,若BD=2,BE=3,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图一条抛物线![]() (a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.

(1)“抛物线三角形”一定是_______________三角形;
(2)若抛物线y=-x2+bx(b>0)的“抛物线三角形”是等腰直角三角形,求b的值;
(3)如图,△OAB是抛物线y=-x2+b′x(b′>0)的“抛物线三角形”,是否存在以原点O为对称中心的矩形ABCD?若存在,求出过O、C、D三点的抛物线的表达式;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙二人用4张扑克牌(分别是红桃2,红桃3,黑桃4,方片5)玩游戏,他们将扑克牌洗匀后,背面朝上放在桌面上,甲先取一张,取出的牌不放回,乙从剩余的牌中取一张.
(1)设![]() 、
、![]() 分别表示甲、乙取出的牌面上的数字,写出
分别表示甲、乙取出的牌面上的数字,写出![]() 的所有结果;
的所有结果;
(2)若甲取到红桃3,则乙取出的牌面数字比3大的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
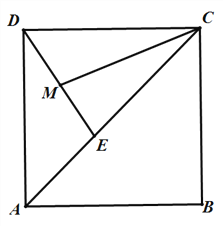
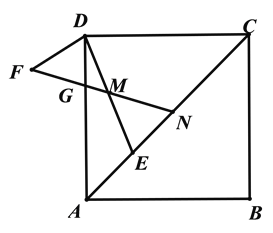
【题目】在菱形ABCD中,AC是对角线,CD=CE,连接DE,点M是线段DE的中点.
(1)如图1,连接CM,若AC=16,CD=10,求DE的长
(2)如图2,点F在菱形的外部,DF=DM,且∠CDA=∠FDE,连接FM交AD于点G,FM的延长线交AC于点N,求证:CN=AG.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com