
����Ŀ����ƽ��ֱ������ϵ�У����Ƕ���ֱ��y=ax��aΪ������![]() ��a��b��cΪ������a��0���ġ�����ֱ�ߡ�����һ���������������ϣ�����һ��������y���ϵ�������Ϊ�䡰���������Ρ���
��a��b��cΪ������a��0���ġ�����ֱ�ߡ�����һ���������������ϣ�����һ��������y���ϵ�������Ϊ�䡰���������Ρ���
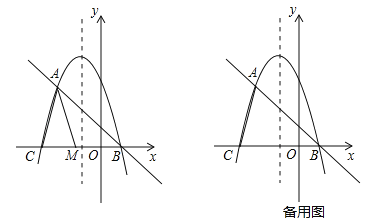
��֪������![]() ���䡰����ֱ�ߡ�����A��B���㣨��A�ڵ�B����ࣩ����x�Ḻ���ύ�ڵ�C��
���䡰����ֱ�ߡ�����A��B���㣨��A�ڵ�B����ࣩ����x�Ḻ���ύ�ڵ�C��
��1����գ��������ߵġ�����ֱ�ߡ��Ľ���ʽΪ ����A������Ϊ ����B������Ϊ ��
��2����ͼ����MΪ�߶�CB��һ���㣬����ACM��AM����ֱ��Ϊ�Գ��ᷭ�ۣ���C�ĶԳƵ�ΪN������AMNΪ�������ߵġ����������Ρ������N�����ꣻ
��3������E�������ߵĶԳ������˶�ʱ���ڸ������ߵġ�����ֱ�ߡ��ϣ��Ƿ���ڵ�F��ʹ���Ե�A��C��E��FΪ������ı���Ϊƽ���ı��Σ������ڣ���ֱ��д����E��F�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��![]() ������2��
������2�� ![]() ������1��0������2��N��������0��
������1��0������2��N��������0�� ![]() ��3����
��3����![]() ��
�� ![]() ������3��E����1����
������3��E����1����![]() ����F��0��
����F��0�� ![]() ����E����1����
����E����1����![]() ����F����4��
����F����4�� ![]() ����
����
�������������������1��������ֱ�ߵĶ������������ʽ����������ֱ���������߽���ʽ�����A��B�����ꣻ
��2����N����y����ʱ����A��AD��y���ڵ�D�����֪AN=AC�����A�����꣬������ON�ij��������N�����ꣻ��M����y���ϼ�M����ԭ��ʱ����N��NP��x���ڵ�P���������������NMP=60������Rt��NMP�У������MP��NP�ij���������N�����ꣻ
��3����ACΪƽ���ı��ε�һ��ʱ����F���Գ���Ĵ���FH����A��AK��x���ڵ�K����֤��EFH�ա�ACK�������DF�ij���������F��ĺ����꣬�Ӷ������F�����꣬��HE�ij������E�����ꣻ��ACΪƽ���ı��εĶԽ���ʱ����E����1��t������A��C������ɱ�ʾ��AC�е㣬�Ӷ��ɱ�ʾ��F������꣬����ֱ��AB�Ľ���ʽ�����t��ֵ�������E��F�����꣮
��1����������![]() ����������ֱ�ߵĽ���ʽΪ
����������ֱ�ߵĽ���ʽΪ![]() ����������ֱ���������߽���ʽ�ɵ���
����������ֱ���������߽���ʽ�ɵ��� 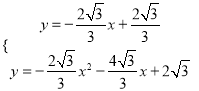 �������
�������  ��
��![]() ����A����2��
����A����2�� ![]() ����B��1��0�����ʴ�Ϊ��
����B��1��0�����ʴ�Ϊ�� ![]() ������2��
������2�� ![]() ������1��0����
������1��0����
��2������N��y����ʱ����AMNΪ���������Σ���ͼ1����A��AD��y���ڵ�D����AD=2����![]() �У���y=0�����x=��3��x=1����C����3��0������A����2��
����y=0�����x=��3��x=1����C����3��0������A����2�� ![]() ������AC=
������AC=![]() =
=![]() ���ɷ��۵����ʿ�֪AN=AC=
���ɷ��۵����ʿ�֪AN=AC=![]() ����Rt��AND�У��ɹ��ɶ����ɵ�DN=
����Rt��AND�У��ɹ��ɶ����ɵ�DN=![]() =
=![]() =3����OD=
=3����OD=![]() ����ON=
����ON=![]() ��3��ON=
��3��ON=![]() +3����ON=
+3����ON=![]() +3ʱ����MN��OD��CM����MN=CMì�ܣ��������⣬��N������Ϊ��0��
+3ʱ����MN��OD��CM����MN=CMì�ܣ��������⣬��N������Ϊ��0�� ![]() ��3����
��3����
��M����y����ʱ����M��O�غϣ���N��NP��x���ڵ�P����ͼ2����Rt��AMD�У�AD=2��OD=![]() ����tan��DAM=
����tan��DAM=![]() =
=![]() �����DAM=60������AD��x�ᣬ���AMC=��DAO=60���������۵���֪��NMA=��AMC=60�������NMP=60������MN=CM=3����MP=
�����DAM=60������AD��x�ᣬ���AMC=��DAO=60���������۵���֪��NMA=��AMC=60�������NMP=60������MN=CM=3����MP=![]() MN=
MN=![]() ��NP=
��NP=![]() MN=
MN=![]() ������ʱN������Ϊ��
������ʱN������Ϊ��![]() ��
�� ![]() ����
����
���Ͽ�֪N������Ϊ��0�� ![]() ��3����
��3����![]() ��
�� ![]() ����
����
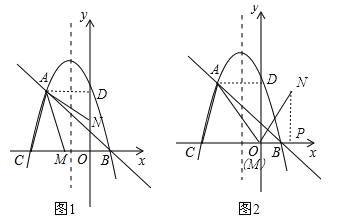

��3������ACΪƽ���ı��εı�ʱ����ͼ3����F���Գ���Ĵ���FH����A��AK��x���ڵ�K������AC��EF��AC=EF�����ACK=��EFH������ACK����EFH�����ߡ�ACK=��EFH����AKC=��EHF��AC=EF�����ACK�ա�EFH��AAS������FH=CK=1��HE=AK=![]() ���������߶Գ���Ϊx=��1����F��ĺ�����Ϊ0��2������F��ֱ��AB�ϣ�����F�������Ϊ0ʱ����F��0��
���������߶Գ���Ϊx=��1����F��ĺ�����Ϊ0��2������F��ֱ��AB�ϣ�����F�������Ϊ0ʱ����F��0�� ![]() ������ʱ��E��ֱ��AB�·�����E��y��ľ���ΪEH��OF=
������ʱ��E��ֱ��AB�·�����E��y��ľ���ΪEH��OF=![]() ��
��![]() =
=![]() ����E����������
����E����������![]() ����E����1����
����E����1����![]() ����
����
��F��ĺ�����Ϊ��2ʱ����F��A�غϣ��������⣬��ȥ��
����ACΪƽ���ı��εĶԽ���ʱ����C����3��0������A����2�� ![]() �������߶�AC���е�����Ϊ����2.5��
�������߶�AC���е�����Ϊ����2.5�� ![]() ������E����1��t����F��x��y������x��1=2������2.5����y+t=
������E����1��t����F��x��y������x��1=2������2.5����y+t=![]() ����x=��4��y=
����x=��4��y=![]() ��t������ֱ��AB����ʽ�ɵ�
��t������ֱ��AB����ʽ�ɵ�![]() ��t=��
��t=��![]() ������4��+
������4��+![]() �����t=��
�����t=��![]() ����E����1����
����E����1����![]() ����F����4��
����F����4�� ![]() ����
����
���Ͽ�֪�������������ĵ�F����ʱE����1���� ![]() ����F��0��
����F��0�� ![]() ����E����1����
����E����1����![]() ����F����4��
����F����4�� ![]() ����
����


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�߶�![]() ��
�� ![]() ��
��![]() ��������ABC��ʹ
��������ABC��ʹ![]() ��
�� ![]() ��
�� ![]() ���ϵ�����
���ϵ�����![]() ������������˳������Ϊ�� ��
������������˳������Ϊ�� ��
���ӳ�![]() ��B��ʹ
��B��ʹ![]() ��������
��������![]() ��������ADC��ʹ
��������ADC��ʹ![]() ��
�� ![]() ��
�� ![]() ��
��
A. �ۢ٢� B. �٢ڢ� C. �ڢۢ� D. �ۢڢ�
���𰸡�A
�������������������������ADC�������ӳ������Ӽ��ɣ�
������֪�������ܹ�ȷ��������������ADC����������ADC��ʹDC=![]() a��AC=b��AD=m�����ӳ�CD��B��ʹBD=CD������AB�����ɵ���ABC��
a��AC=b��AD=m�����ӳ�CD��B��ʹBD=CD������AB�����ɵ���ABC��
�������ĺ���˳��Ϊ�ۢڢ�����ѡA��
���㣺���⿼����ǻ�����ͼ
�����������Ĺؼ�������������֪�����ε����ߺ�����һ���ϵ������������ε�������
�����͡���ѡ��
��������
6
����Ŀ����ͼ����ֱ�ߺ�Բ����һ���ǵ�����֪�ǵ�ʾ��ͼ����˵��![]() �������ǣ� ��
�������ǣ� ��


A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�ı���ABCD�У�AD��BC����BCD=90����AB=BC+AD����DAC=45����EΪCD��һ�㣬����BAE=45������CD=4������ABE�����Ϊ��������

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y=-x+m��ͼ���y�ύ�ڵ�B��������������y=xͼ���ڵ�P ��2��n����
��1����m��n��ֵ��
��2������POB�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ȥ�������в��ֵ��������˺����ĺ��֣���������������������ij��λ��ij����Сѧ����һ������ˮ���߲˹�320������������ˮ���߲˶�80����
��1��������ˮ���߲˸��ж��ټ���
��2���ּƻ����üס������ֻ�����8����һ���Խ���������ˮ���߲�ȫ������������Сѧ����֪ÿ�����ֻ�������װ����ˮ40�����߲�10����ÿ�����ֻ�������װ����ˮ���߲˸�20���������䲿�Ű��żס������ֻ���ʱ�м��ַ��������������Ƴ�����
��3���ڣ�2���������£�������ֻ���ÿ���踶�˷�400Ԫ�����ֻ���ÿ���踶�˷�360Ԫ�����䲿��Ӧѡ�����ַ�����ʹ�˷����٣������˷��Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijˮ�����������ڣ������Ϊ10Ԫ/���ij��ˮ�����������ν��ۺ�ļ۸�Ϊ8.1Ԫ/��������ν��۵İٷ�����ͬ��
��1�������ˮ��ÿ�ν��۵İٷ��ʣ�
��2���ӵ�һ�ν��۵ĵ�1�����𣬵�x�죨xΪ���������ۼۡ��������������ķ��õ������Ϣ�����ʾ����֪����ˮ���Ľ���Ϊ4.1Ԫ/������۸�ˮ����x���죩������Ϊy��Ԫ������y��x��1��x��15��֮��ĺ�����ϵʽ��������ڼ���ʱ�����������

��3���ڣ�2���������£���Ҫʹ��15�������ȣ�2����������������127.5Ԫ�����15���ڵ�14��ļ۸���������ɽ�����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲����и�ʽ
��x��1����x+1��=x2��1��
��x��1����x2+x+1��=x3��1��
��x��1����x3+x2+x+1��=x4��1��
����
��1���������Ϲ��ɣ���x��1����x6+x5+x4+x3+x2+x+1��=�� ����
��2�����ܷ��ɴ˹��ɳ�һ���Թ��ɣ���x��1����xn+xn��1+��+x+1��=�� ����
��3���������Ϲ�����1+3+32+��+334+335�Ľ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������һ����Ȼ������λ�����ִ����λ����λ�����ų�һ�����֣���Ӹ�λ�����λ�����ų���һ��������ȫ��ͬ����ô���ǰ���������Ȼ������ ����г���������磺��Ȼ��64746�����λ����λ�ų���һ�������ǣ�6��4��7��4��6���Ӹ�λ������ų���һ������Ҳ�ǣ�6��4��7��4��6����64746������г���������磺33��181��212��4664��������������г������
��1������ֱ��д��3����λ����г��������������һ����λ����г�����ܷ�11��������˵�����ɣ�[����
��2�� ��֪һ���ܱ�11��������λ����г���������λ�ϵ�����Ϊx��![]() ��xΪ��Ȼ������ʮλ�ϵ�����Ϊy����y��x�ĺ�����ϵʽ��
��xΪ��Ȼ������ʮλ�ϵ�����Ϊy����y��x�ĺ�����ϵʽ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com